Математика 4 класс

Задачи на движение в одном направлении

1. Моторная лодка, двигаясь со скоростью 25 км/ч, прошла путь между пристанями за 2 ч. Сколько потребуется времени, чтобы пройти этот же путь на байдарке, если она движется со скоростью 5 км/ч?2. Ворона летела 3 ч со скоростью 50 км/ч. Сколько потребуется времени скворцу, чтобы пролететь это же расстояние со скоростью 75 км/ч?3. Пешеход шёл со скоростью 6 км/ч и был в пути 6 ч. Сколько времени понадобится, чтобы пройти такое же расстояние лыжнику, скорость которого 12 км/ч?4. Чёрный стриж, двигаясь со скоростью 120 км/ч, был в пути 2 ч. Сколько потребуется времени галке, чтобы пролететь это же расстояние со скоростью 60 км/ч?5. Машина «скорой помощи», двигаясь со скоростью 120 км/ч, была в пути 2 ч. Сколько потребуется времени автомобилю «Запорожец», чтобы проехать этот же путь со скоростью 60 км/ч?6. Гепард пробежал 3 ч со скоростью 100 км/ч. Сколько потребуется времени слону, чтобы пробежать это же расстояние, если его скорость равна 50 км/ч?7. Вёсельная лодка, двигаясь со скоростью 5 км/ч, была в пути 6 ч. За какое время можно проплыть этот путь на катамаране со скоростью 15 км/ч?8. Путь между двумя деревнями мальчик проходит за 5 ч со скоростью 4 км/ч. За какое время он проезжает этот путь на велосипеде со скоростью 10 км/ч?9. Эскимосская собака бежала 60 с со скоростью 15 м/с. За какое время может пробежать этот путь гончая собака, двигаясь со скоростью 30 м/с?10. Рыба-меч, двигаясь со скоростью 70 км/ч, была в пути 2 ч. За какое время может проплыть этот путь скумбрия, двигаясь со скоростью 20 км/ч?

Простые задачи на движение

1. Мотоциклист за 4 ч проехал 320 км. С какой скоростью ехал мотоциклист?2. Самолёт пролетел 1800 км за 3 ч. С какой скоростью летел самолёт?3. Комар пролетел 16 дм со скоростью 4 дм/с. Сколько времени комар был в полёте?4. Катер за 3 ч проплыл 96 км. С какой скоростью плыл катер?5. Почтовый голубь за 3 ч пролетел 270 км. С какой скоростью летел почтовый голубь?6. За 4 с бегемот пробежал 48 м. С какой скоростью бежал бегемот?7. Товарный поезд за 2 ч проехал 70 км. С какой скоростью шёл поезд?8. Паук за 2 с пробежал 60 см. С какой скоростью бежал паук?9. Жук за 2 ч пролетел 22 км. С какой скоростью летел жук?10. Лыжник со скоростью 8 км/ч прошёл дистанцию 24 км. За сколько времени лыжник прошёл эту дистанцию?

Теперь озвучиваем основные правила:

1. Умножаем, складываем, делим или вычитаем;
   Математика 2 класс

   Выполняем то, что можно сделать, уравнение станет немного короче.

2. Х в одну сторону, цифры в другую.

   Неизвестную переменную в одну сторону (не всегда это х, может быть и другая буква), числа в другую.

3. При переносе х или цифры через знак равенства, их знак меняется на противоположный.

    Если было число положительным, то при переносе перед цифрой ставим знак минус. И наоборот, если число или х было со знаком минус, то при переносе через равно ставим знак плюс.

4. Если в конце уравнение начинается с числа, то просто меняем местами.
5. Всегда делаем проверку!

При выполнении домашнего задания, классной работы, тестов, всегда можно взять лист и написать вначале на нём и сделать проверку.

Дополнительно находим подобные примеры в интернете, дополнительных книгах, методичках. Проще не менять цифры, а брать уже готовые примеры.

Чем больше ребёнок будет решать сам, заниматься самостоятельно, тем быстрее усвоит материал.

Если ребенок не понимает примеры с уравнением, стоит объяснить пример и сказать, чтобы остальные делал по образцу.

Данное подробное описание, как объяснить уравнения с х школьнику для:

• родителей;
• школьников;
• репетиторов;
• бабушек и дедушек;
• учителей;

Детям нужно все делать в цвете, разными мелками на доске, но увы не все так делают.

Задачи на встречное движение

1. Из двух городов одновременно вылетели навстречу друг другу два голубя. Они встретились через 5 ч. Скорость одного голубя 62 км/ч, а второго 68 км/ч. Узнай расстояние между городами.2. Из двух посёлков одновременно выехали навстречу друг другу велосипедист и мотоциклист. Они встретились через 4 ч. Скорость велосипедиста 15 км/ч, а мотоциклиста 57 км/ч. Узнайрасстояние между посёлками.3. От двух пристаней одновременно навстречу друг другу отошли катер и лодка. Они встретились через 6 ч. Скорость лодки 8 км/ч, а скорость катера 35 км/ч. Узнай расстояние между пристанями.4. Две морские звезды одновременно поползли из своих укрытий навстречу друг другу. Первая ползла со скоростью 5 дм/ч, а вторая со скоростью 4 дм/ч. Встретились они через 2 ч. Узнай расстояние между укрытиями морских звёзд. 5. Две девочки вышли одновременно навстречу друг другу из своих домов. Они встретились через 8 мин. Одна шла со скоростью 60 м/мин, а другая со скоростью 70 м/мин. Каково расстояние между домами девочек?6. Два автомобилиста выехали одновременно из двух городов навстречу друг другу. Скорость одного автомобилиста 80 км/ч, а скорость другого 100 км/ч. Узнай расстояние между городами, если автомобилисты встретились через 3 ч.7. Две гремучие змеи выползли одновременно из своих укрытий навстречу друг другу и встретились через 5 мин. Скорость одной змеи 48 м/мин, а скорость другой 53 м/мин. Каково расстояние между укрытиями змей?8. Из двух гнёзд одновременно навстречу друг другу вылетели два ястреба. Встретились они через 6 с. Скорость одного ястреба 6 м/с, скорость другого 16 м/с. Каково расстояние между гнёздами ястребов?9. Из двух городов навстречу друг другу одновременно выехали два мотоциклиста. Встретились они через 4 ч. Скорость одного мотоциклиста 85 км/ч, скорость другого 95 км/ч. Каково расстояние между городами?10. Два пешехода вышли одновременно из двух деревень навстречу друг другу. Один шёл со скоростью 5 км/ч, скорость другого 4 км/ч. Через сколько часов они встретятся, если расстояние между деревнями 36 км?

Пример № 2

Пример уравнения для 4 класса со знаком минус.

Х – 180 = 240/3

Первым действием смотрим, что мы можем сделать в этом уравнении?  В данном примере мы можем разделить. Производим деление 240 разделить на 3 получаем 80. Переписываем уравнение ещё раз.

Х – 180 = 80 (выделила цифры зеленым маркером).

Теперь мы видим, что у нас есть х (неизвестное) и числа, только не рядом, а разделяет их знак равно. Х в одну сторону, цифры в другую.

Х = 80 + 180  Знак плюс ставим потому что при переносе числа, знак что был перед цифрой меняется на противоположный. Считаем.

Х = 260  Выполняем проверочную работу. Проверка покажет правильно ли мы решили уравнение. Вместо х вставляем число, которое получили.

Описание

Программа «Задание на неделю 4 класс» формирует задачи и примеры по математике, которые помогут закрепить ребенку все знания, полученные в четвертом классе в течение года, а также подготовится к проверочной и контрольной работе.

На листе формата А4 формируется 13 заданий по математике. При этом задания даются в небольшом объеме, но с максимальным охватом всех типов примеров. Это позволяет детям быстро вспомнить материал 4 класса.

В каждую карточку входят следующие виды заданий:

• чередующиеся задания, включающее:
  • • задание на повторение понятий «сумма», «разность», «произведение» и «частное» с вычислениями;
    • примеры на нахождение сторон, периметра и площади прямоугольника;
    • простые задачи на движение: нахождение скорости, времени или расстояния.
• примеры на сложение, вычитание, умножение и деление, в том числе: логические (вставить знаки для получения верного равенства),
• выражения на порядок действий (от пяти действий со скобками);
• примеры на умножение и деление разных типов: умножение и деление круглых чисел, внетабличное умножение и деление;
• примеры на деление с остатком с вычисление частного, уменьшаемого или вычитаемого;
• решение уравнений;
• задание на сравнение дробей (долей)
• задание на нахождение части от числа (от суммы, разности, произведения или частного);
• задания на повторение единиц измерения длины, массы и времени;
• задание на нахождение доли и процентов от единиц измерения: длины, площади, массы и времени;
• примеры в столбик: сложение трехзначных чисел, вычитание трехзначных чисел, умножение двухзначного числа на однозначное, умножение трехзначного числа на однозначное и двузначное, на однозначное число.

Программа «Задание на неделю 4 класс» написана в Excel с помощью макросов. Данные генерируются случайным образом, что позволяет получить более тысячи вариантов заданий для 4 класса, карточки заданий не повторяются.

Для ознакомления с программой можно скачать изображение карточки, которая получилась с помощью программы. Для получения новой карточки математического диктанта достаточно скачать, нажать на кнопку и распечатать.

Другие программы, которые помогут закрепить навыки счета:

• Цепочки примеров в пределах 1000 (все действия)
• Числовые пирамиды большие (в пределах 50,100 и больше)
• Умножение и деление по типам (табличное, внетабличное, круглых чисел)
• Сложение и вычитание в столбик
• Умножение и деление в столбик
• Деление с остатком на число (с выбором уровня сложности)
• Порядок действий в пределах 1000 (все действия)
• Сложные примеры на порядок действий
• Выражения с именованными числами

Задачи на нахождение площади

1. Найдите площадь и периметр прямоугольника со сторонами 8 см и 9 см. 679. Длина прямоугольника 7 дм, ширина 3 дм. Чему равны площадь и периметр прямоугольника?2. Площадь фундамента дома квадратной формы 64 кв. м. Чему равен периметр дома?3. Длина прямоугольника 6 дм, ширина 4 см. Чему равны площадь и периметр прямоугольника?4. Длина прямоугольника 4 м, ширина 3 дм. Чему равны площадь и периметр прямоугольника? 5. Ширина вагона 3 м, а длина 750 см. Чему равны площадь и периметр вагона?6. Высота зеркала 180 см, ширина 70 см. Чему равны площадь и периметр зеркала?7. Длина прямоугольника равна стороне квадрата с периметром 48 см, а ширина его в 4 раза меньше. Чему равны площади прямоугольника и квадрата?8. Чему равны площади всех возможных прямоугольников с периметром 18 см, если длина их сторон выражена целым числом сантиметров. У какого прямоугольника площадь наибольшая?9. Детская площадка была длиной 16 м и шириной 14 м. После переделки её увеличили в длину на 4 м и уменьшили в ширину на 3 м. Как изменилась площадь детской площадки?10. Сколько краски пойдёт на окраску пола длиной 8 м и шириной 6 м, если на окраску 1 кв. м требуется 150 г краски?

Задачи на противоположное движение

1. От одного улья одновременно в противоположных направлениях вылетели две пчелы со скоростью 7 м/с и 6 м/с. Какое расстояние будет между ними через 45 с?2. От одной пристани одновременно в противоположных направлениях вышли два катера со скоростью 32 км/ч и 38 км/ч. Какое расстояние будет между ними через 7 ч?3. С лыжной базы одновременно в противоположных направлениях вышли два лыжника. Через 2 ч расстояние между ними было 60 км. Чему равна скорость второго лыжника, если скорость первого 14 км/ч?4. Из гаража одновременно в противоположных направлениях вышли две автомашины. Одна шла со скоростью 50 км/ч. Через 4 ч расстояние между ними было 480 км. Чему равна скорость второй автомашины?5. С одного аэродрома одновременно в противоположных направлениях вылетели самолёт и вертолёт. Скорость вертолёта 230 км/ч. Через 5 ч расстояние между ними было 4250 км. Найди скорость самолёта.6. Из одного места одновременно в противоположных направлениях вылетели два комара. Через 25 с расстояние между ними было 1850 см. Найди скорость одного из комаров, если скорость другого 38 см/с?7. Из одного города одновременно в противоположных направлениях выехали два автобуса. Через 3 ч расстояние между ними было 243 км. Чему равна скорость первого автобуса, если скорость второго 45 км/ч?8. Из одного укрытия одновременно в противоположных направлениях поплыли две морские змеи. Через 13 мин расстояние между ними было 1066 м. Найди скорость одной из морских змей, если скорость другой 40 м/мин?9. Из одного посёлка одновременно в противоположных направлениях выехали автомобиль и автобус. Через 2 ч расстояние между ними было 310 км. Найди скорость автомобиля, если скорость автобуса 65 км/ч.10. С аэродрома вылетели в одно и то же время в противоположных направлениях два самолёта. Один из них летел со скоростью 640 км/ч, а другой со скоростью 570 км/ч. Какое расстояние будет между ними через 3 ч?

Сложноподчиненное предложение

Сложноподчиненное предложение (СПП) — это вид сложного предложения, в составе которого одно простое предложение по смыслу и интонации подчиняется другому. В этом случае зависимое предложение называется придаточным, а независимое — главным.

Пример сложноподчиненного предложения:

Мне было сложно понять, как ей удалось так быстро привыкнуть к новому городу.

Виды связи в сложноподчиненном предложении

Обычно части СПП в русском языке связаны друг с другом подчинительными союзами, например:

Я только-только закончил картину, когда солнце уже готовилось потухнуть.

Бывают сложные предложения, в которых придаточное с главным связаны только по смыслу и разделены знаком препинания, но между ними все еще можно вставить подчинительный союз. Такие предложения называют бессоюзными.

Пример:

На меня нахлынуло осознание: (что) все это время меня обманывали

Значения придаточных предложений в СПП

Придаточные предложения в составе сложных делятся на группы, а далее — на подгруппы по смыслу и виду связи с главным.

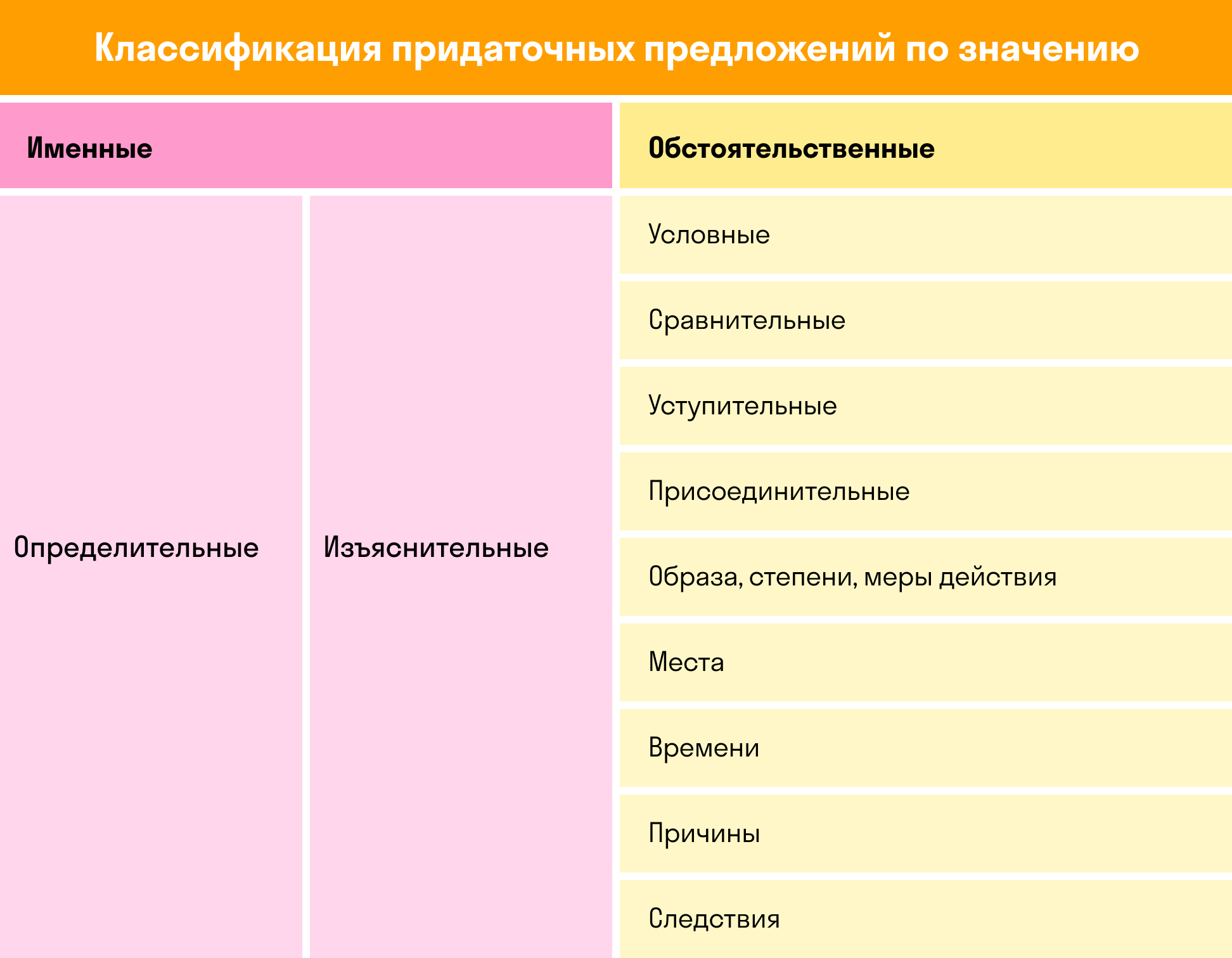
Подробнее о различиях между придаточными в сложном предложении с примерами можно прочесть в этой статье.

Типы подчинения в сложноподчиненном предложении

Иногда в сложноподчиненном предложении не одно, а два и более придаточных. Такой вид сложных предложений называют многочленными. Для них справедливы разные типы подчинения.

Подробнее эту тему мы уже разбирали в статье о сложноподчиненных предложениях.

Знаки препинания в сложноподчиненных предложениях

Между главной и придаточной частями сложного предложения принято ставить запятую. Если одна часть стоит в середине другой, выделять запятой ее нужно с обеих сторон:

• Когда мы вернулись в город, все горести остались за плечами.

• Сейчас, когда мы вернулись в город, все горести остались за плечами.

Если предложения со словами лишь, только, еще и, прежде всего, именно, очевидно, вероятно связаны составным союзом, он разделяется. Тогда перед словом что нужно ставить запятую:

Он согласился лишь потому, что я хорошо попросила.

Если мы выделяем интонацией изъявительные или условные придаточные и ставим их перед главным предложением, между ними ставится тире:

Кто желает — тот получит.

Если по главному предложению понятно, что придаточное его пояснит, нужно ставить двоеточие. То же правило относится и к бессоюзным сложным предложениям:

Он вдруг осознал: дальше не стоит и пытаться.

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+)
• вычитание (-)
• умножение (*)
• деление (:)

Операции отношения:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
• 3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.

Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.

Возведение степень — операция умножения числа на самого себя несколько раз.

Основание степени — число, которое повторяется сомножителем определённое количество раз.

Показатель степени — число, которое указывает, сколько раз берется одинаковый множитель.

Степенью называется число, которое получается в результате взаимодействия основания и показателя степени.

• Запись: 34 = 81, где 3 — основание степени, 4 — показатель степени, 81 — степень.
• 3^4 = 3 * 3 * 3 * 3

Вторая степень называется квадратом, третья степень — кубом. Первой степенью числа называют само это число.

Извлечение корня — арифметическое действие, обратное возведению в степень.

• Запись: 4√81 = 3, где 81 — подкоренное число, 4 — показатель корня, 3 — корень.
• З^4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
• 2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

Движение в противоположных направлениях

Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:

Скорость удаления больше скорости любого из них.

Задача 1

Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?

Решение:

Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.

1. 

Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.

2. 

Ответ: Через три часа расстояние между переходами будет 27 км.

Задача 2

Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?

Решение:

Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:

1. 

Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.

2. 

Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.

3. 

Ответ: Скорость второго пешехода – 4 км/ч.

Задача 3

Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?

Решение:

1) 70+45=115 (км/ч) скорость удаления поездов

2) 115∙2=230 (км) пройдут поезда вместе за 2 часа

3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.

Ответ: Через 2 часа расстояние между поездами составит 250 км.

Задача 4

Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?

Решение:

1) 60+40=100 (км/ч) скорость удаления мотоциклистов

2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.

Признак делимости на 4, примеры

Мы можем пойти простым путем и поделить однозначное натуральное число на 4 для того, чтобы проверить, делится ли это число на 4 без остатка. Так же можно поступить с двузначными, трехзначными и проч. числами.  Однако, чем больше становятся числа, тем сложнее проводить с ними действия с целью проверки делимости их на 4.

Гораздо проще становится использовать признак делимости на 4. Он предполагает проведение проверки делимости одной или двух последних цифр целого числа на 4. Что это значит? Это значит, что некоторое число a делится на 4 в том случае, если одна или две крайние правые цифры в записи числа a делятся на 4. Если число, составленное из двух крайних правых цифр в записи числа a не делятся на 4 без остатка, то и число a не делится на 4 без остатка.

Пример 1

Какие из чисел 98 028, 7 612 и 999 888 777 делятся на 4?

Решение

Крайние правые цифры чисел − 98 028, 7 612 составляют числа 28 и 12, которые делятся на 4 без остатка. Это значит, что и целые числа − 98 028, 7 612​​​​​​ ​делятся на 4 без остатка.

Последние две цифры в записи числа 999 888 777 образуют число 77, которое не делится на 4 без остатка. Это значит, что и исходное число на 4 без остатка не делится.

Ответ: −98 028 и 7 612.

Если предпоследней цифрой в записи числа является , то нам необходимо этот ноль отбросить и смотреть на оставшуюся крайнюю правую цифру в записи. Получается, что две цифры 01 мы заменяем 1. И уже по одной оставшейся цифре мы делаем вывод о том, делится ли исходное число на 4.

Пример 2

Делится ли числа 75 003 и −88 108 на 4?

Решение

Две последние цифры числа 75 003 — видим 03. Если отбросить ноль, то у нас остается цифра 3, которая на 4 без остатка не делится. Это значит, что исходное число 75 003 на 4 без остатка не делится.

Теперь возьмем две последние цифры числа −88 108. Это 08, из которых мы должны оставить лишь последнюю цифру 8. 8 делится на 4 без остатка.

Это значит, что и исходное число −88 108 мы можем поделить на 4 без остатка.

Ответ: 75 003 не делится на 4, а −88 108 – делится.

Числа, у которых в конце записи идет сразу два нуля, также делятся на 4 без остатка. Например, 100 делится на 4, получается 25. Доказать правдивость этого утверждения нам позволяет правило умножения числа на 100.

Представим произвольно выбранное многозначное число a, запись которого справа заканчивается двумя нулями, как произведение a1·100, где число a1 получается из числа a, если в его записи справа отбросить два нуля. Например, 486700=4867·100.

Произведение a1·100 содержит множитель 100, который делится на 4. Это значит, что все приведенное произведение делится на 4.

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Определение 3

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 4

Условие: вычислите, сколько будет 5+(7−2·3)·(6−4)2.

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7−2·3. Здесь нам надо умножить 2 на 3 и вычесть результат из 7:

7−2·3=7−6=1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6−4=2.

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5+(7−2·3)·(6−4)2=5+1·22

Начнем с умножения и деления, потом выполним вычитание и получим:

5+1·22=5+22=5+1=6

На этом вычисления можно закончить.

Ответ: 5+(7−2·3)·(6−4)2=6.

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Пример 5

Условие: вычислите, сколько будет 4+(3+1+4·(2+3)).

Решение

У нас есть скобки в скобках. Начинаем с 3+1+4·(2+3), а именно с 2+3. Это будет 5. Значение надо будет подставить в выражение и подсчитать, что 3+1+4·5. Мы помним, что сначала надо умножить, а потом сложить: 3+1+4·5=3+1+20=24. Подставив найденные значения в исходное выражение, вычислим ответ: 4+24=28.

Ответ: 4+(3+1+4·(2+3))=28.

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет (4+(4+(4−62))−1)−1. Начинаем с выражения во внутренних скобках. Поскольку 4−62=4−3=1, исходное выражение можно записать как (4+(4+1)−1)−1. Снова обращаемся к внутренним скобкам:  4+1=5. Мы пришли к выражению (4+5−1)−1. Считаем 4+5−1=8 и в итоге получаем разность 8-1, результатом которой будет 7.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Как решаем:

1. Перенесем 6x из левой части в правую. Знак меняем на противоположный, то есть минус.

   6x −5x = 10

2. Приведем подобные и завершим решение.

   x = 10

Ответ: x = 10.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Как решаем:

1. Сократим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

   −4x = 12 | :(−4)
   x = −3

Ответ: x = −3.

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Как решаем:

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

2 + 3 = 5.

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Задачи на нахождение числа по доле и доли по числу

1. Руда на 4/5 состоит из меди. Сколько меди можно получить из одной тонны руды?2. 15 см — это 2/3 доски. Чему равна длина всей доски?3. При помоле на ржаную муку отходит в отруби 2/5 веса зерна. Сколько отрубей и сколько ржаной муки получится при помоле двух тонн зерна?4. Какой длины потребуется доска для прямоугольной рамки, если длина рамки 28 см, а ширина 4/7 длины?5. Длина дома 12 м, а ширина составляет 4/6 длины. Чему равен периметр дома?6. От мотка проволоки отрезали 2/5. Это 12 м. Чему равна длина всей проволоки?7. Сколько дней составляет 5/6 апреля?8. 4/5 кружки сахарного песка весят 200 г. Сколько весит кружка сахарного песка? 9. книге 68 страниц. Мальчик прочитал 3/4 книги. Сколько страниц осталось прочитать мальчику?10. В спортивной секции занимается 24 мальчика и несколько девочек. Число девочек составляет 3/8 числа мальчиков. Сколько всего человек занимается в спортивной секции?

Задачи на движение в обратном направлении

1. Расстояние между городами 504 км. Сколько времени потребуется машине на проезд туда и обратно, если скорость машины в одном направлении 63 км/ч, а в обратном на 21 км/ч больше?2. Расстояние между пристанями в 40 км лодка прошла за 5 ч. На обратном пути её скорость увеличилась на 2 км/ч. За какое время лодка пройдёт весь путь туда и обратно?3. Мальчики прошли до деревни 30 км, двигаясь со скоростью 5 км/ч, а обратно они ехали на велосипеде в 2 раза быстрее. За сколько часов они проехали это расстояние?4. Расстояние между двумя пристанями 45 км. Катамаран прошёл его за 3 ч, на обратном пути его скорость уменьшилась на 6 км/ч. Сколько времени катамаран потратил на путь туда и обратно?5. Расстояние между пристанями 480 км. Катер «Метеор» прошёл его за 6 ч. На обратном пути его скорость увеличилась на 16 км/ч. За какое время катер «Метеор» пройдёт весь путь туда и обратно?6. Божья коровка пролетела до места приземления 3 мин со скоростью 80 см/мин. После этого ей осталось пролететь в 2 раза меньше, и на этот путь она потратила 2 мин. С какой скоростью полетела божья коровка оставшийся путь?7. Путь от города до посёлка, равный 60 км, велосипедист проехал за 4 ч. На обратном пути он уменьшил скорость на 5 км/ч. Сколько времени велосипедист потратил на путь туда и обратно?8. Расстояние между пристанями в 200 км теплоход прошёл за 5 ч. На обратном пути его скорость уменьшилась в 2 раза. За какое время теплоход пройдёт весь путь туда и обратно?9. Баржа проплыла против течения расстояние 84 км за 7 ч, а на обратном пути её скорость увеличилась на 9 км/ч. Сколько времени она потратила на путь туда и обратно?10. Машина шла до остановки 5 ч со скоростью 68 км/ч. После этого ей осталось проехать вдвое меньший путь, на который она потратила 2 ч. С какой скоростью ехала машина после остановки?

Пример № 1

Пример уравнения для 4 класса со знаком плюс.

Х + 320 =80*7

Самым первым действием смотрим, что мы можем сделать в этом уравнении? Тут мы можем выполнить умножение. Умножаем 80*7 получаем 560. Переписываем ещё раз.

Х + 320 = 560 (выделила цифры зеленым маркером).

Теперь мы видим, что у нас есть х (неизвестное) и числа, только не рядом, а разделяет их знак равно. Х в одну сторону, цифры в другую.

Х = 560 – 320. Минус ставим потому что при переносе числа, знак что перед ним меняется на противоположный. Выполняем вычитание.

Х = 240 Обязательно делаем проверку. Проверка покажет правильно ли мы решили уравнение. Вместо х вставляем число, которое получили.

Проверка:

240 + 320 = 80*7  Складываем числа, с другой стороны умножаем.

560 = 560.

Всё верно! Значит мы решили уравнение правильно!