Тесты. математика 3 класс. табличное умножение и деление чисел

Что важнее – умножение или сложение?

При решении примеров Расставь порядок действий. Умножить или разделить – на первом месте.

Для выражений, в которых присутствуют не сложение либо вычитание, а умножение или деление, действует то же правило: все действия с числами выполняются по порядку, начиная с левого:

81 : 9 х 2 = ?

1. 81 : 9 = 9;
2. 9 х 2 = 18.

Сложнее случай – когда в одной задаче встречаются умножение или деление со сложением или вычитанием. Каков порядок вычислений тогда?

Рассмотрим пример:

8 : 2 + 2 = ?

Если выполнять все действия по порядку, сначала деление, затем сложение. В итоге получим:

1. 8 : 2 = 4;
2. 4 + 2 = 6.

Правило третье: Если в задаче необходимо произвести умножение или деление, они выполняются в первую очередь.

Значит, пример решен правильно. А если в нем будут скобки?

8 : (2 + 2) = ?

1. 2 + 2 = 4;
2. 8 : 4 = 2.

То, что заключено в скобки, всегда в приоритете. Для того они и стоят в выражении. Поэтому порядок вычислений в подобных выражениях будет следующим:

1. Раскрываем скобки. Если их несколько, делаем вычисления для каждых.
2. Умножение либо деление.
3. Вычисляем конечный результат, выполняя действия слева направо.

Пример:
81 : 9 + (6 – 2) + 3 = ?

1. 6 – 2 = 4;
2. 81 : 9 = 9;
3. 9 + 4 = 13;
4. 13 + 3 = 16.

81 : 9 + (6 – 2) + 3 = 16.

А что будет приоритетным: умножение — или деление, вычитание — или сложение, если оба действия встречаются в задаче? Ничего, они равны, в таком случае действует первое правило – действия производятся одно за другим, начиная слева.

Алгоритм решения выражения:

1. Анализируем задачу – есть ли скобки, какие математические действия нужно будет выполнить.
2. Выполняем вычисления в скобках.
3. Делаем умножение и деление.
4. Выполняем сложение и вычитание.

Пример:

28 : (11 – 4) + 18 – (25 – 8) = ?

Порядок вычисления:

1. 11 – 4 = 7;
2. 25 – 8 = 17;
3. 28 : 7 = 4;
4. 4 + 18 = 22;
5. 22 – 17 = 5.

Ответ: 28 : (11 – 4) + 18 – (25 – 8) = 5.

Важно! Если в выражении есть буквенные обозначения, порядок действий остается прежним

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+)
• вычитание (-)
• умножение (*)
• деление (:)

Операции отношения:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
• 3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.

Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.

Возведение степень — операция умножения числа на самого себя несколько раз.

Основание степени — число, которое повторяется сомножителем определённое количество раз.

Показатель степени — число, которое указывает, сколько раз берется одинаковый множитель.

Степенью называется число, которое получается в результате взаимодействия основания и показателя степени.

• Запись: 34 = 81, где 3 — основание степени, 4 — показатель степени, 81 — степень.
• 3^4 = 3 * 3 * 3 * 3

Вторая степень называется квадратом, третья степень — кубом. Первой степенью числа называют само это число.

Извлечение корня — арифметическое действие, обратное возведению в степень.

• Запись: 4√81 = 3, где 81 — подкоренное число, 4 — показатель корня, 3 — корень.
• З^4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
• 2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

Задачи на темы: “Порядок выполнения действий. Расстановка скобок”

1. Реши примеры.

1.1) 35 : 5 + ( 23 + 7 ) : 5 – 3 * 4 =
1.2) ( 39 – 19 ) * 3 + 24 : 3 + ( 9 + 36 ) : 5 – 13 =
1.3) 760 – (14 + 31 ) : 5 – 6 * 3 + 41 =
1.4) ( 52 – 34) : 2 * 8 + 7 * 3 – 13 + ( 64 – 44 ) : 4 =
1.5) ( 87 – 79 ) * 9 : 3 + 9 * 6 =
1.6) 45 : 9 + ( 13 + 22 ) : 5 + 4 * 6 =
1.7) 8 * 5 – 14 : 7 : 2 – ( 42 – 24 ) : 6=
1.8) 70 – ( 15 + 24 : 3) + 4 * 3 + 8 * 2=
1.9) 5 * 3 + 7 * 4 – (1 + 9) : 2 * 6 =

2. Расставь правильно скобки.

2.1) 3 + 6 : 3 + 3 * 3 = 6
2.2) 3 + 6 : 3 + 3 * 3 = 14
2.3) 3 + 6 : 3 + 3 * 3 = 12
2.4) 3 + 6 : 3 + 3 * 3 = 18

3. Расставь скобки различными способами и реши получившиеся примеры.

3.1) 5 + 5 – 5 * 5 + 5 =
3.2) 5 + 5 – 5 * 5 + 5 =
3.3) 5 + 5 – 5 * 5 + 5 =
3.4) 5 + 5 – 5 * 5 + 5 =
3.5) 6 * 6 – 6 + 6 : 6 =
3.6) 6 * 6 – 6 + 6 : 6 =
3.7) 6 * 6 – 6 + 6 : 6 =
3.8) 6 * 6 – 6 + 6 : 6 =
3.9) 7 – 7 * 7 + 7 : 7 =
3.10) 7 – 7 * 7 + 7 : 7 =
3.11) 7 – 7 * 7 + 7 : 7 =
3.12) 7 – 7 * 7 + 7 : 7 =

4. Расставь скобки разными способами и реши получившиеся примеры.

4.1) 12 : 4 + 56 : 7 – 36 : 6 + 13 =
a) __________
б) __________
в) __________
г) __________
4.2) 32 + 18 : 3 + 14 * 3 + 81 : 9 =
a) __________
б) __________
в) __________
г) __________
4.3) 56 : 8 + 8 * 5 – 72 : 8 =
a) __________
б) __________
в) __________
г) __________

Простые задачи на нахождение цены

1. 6 одинаковых мочалок для посуды стоят 12 руб. Сколько стоит одна мочалка для посуды?2. 2 пачки хлебцев стоят 16 руб. Узнай цену пачки хлебцев. 3. 2 одинаковые расчёски для волос стоят 18 руб. Сколько стоит одна расчёска?4. Папа за 8 л бензина заплатил 72 руб. Сколько стоит 1 л бензина?5. За 3 одинаковые нити мишуры заплатили 30 руб. Узнай цену одной нити мишуры. 6. Тётя Люся за 5 пакетов сливок заплатила 50 руб. Узнай цену одного пакета сливок.7. 4 банки майонеза стоят 36 руб. Сколько стоит одна банка майонеза?8. За 3 банки томатной пасты заплатили 12 руб. Сколько стоит одна банка томатной пасты?9. За 7 электрических лампочек заплатили 42 руб. Сколько стоит одна электрическая лампочка?10. За 2 одинаковых фляжки для воды заплатили 16 руб. Сколько стоит одна фляжка?

Описание

Программа «Задание на неделю 3 класс» формирует задачи и примеры, которые помогают закрепить ребенку все знания, полученные во третьем классе в течение года, а также подготовится к проверочной и контрольной работе.

На листе формата А4 формируется 13 заданий по математике. При этом задания даются в небольшом объеме, но с максимальным охватом всех типов примеров. Это позволяет детям быстро вспомнить материал 3 класса.

В каждую карточку входят следующие виды заданий:

• задание на повторение понятий «слагаемое», «сумма», «уменьшаемое», «вычитаемое», «разность», «множитель», «произведение», «делимое», «делитель» и «частное» с вычислениями;
• примеры на сложение, вычитание, умножение и деление, в том числе: логические (вставить знаки для получения верного равенства),
• выражения на порядок действий (от пяти действий со скобками);
• примеры на умножение и деление разных типов: умножение и деление круглых чисел, внетабличное умножение и деление;
• примеры на деление с остатком с вычисление частного, уменьшаемого или вычитаемого;
• решение уравнений;
• задание на сравнение дробей (долей) и нахождение части от числа;
• задания на повторение единиц измерения длины, массы и времени;
• примеры в столбик: сложение трехзначных чисел, вычитание трехзначных чисел, умножение двухзначного числа на однозначное, умножение трехзначного числа на однозначное и двузначное, на однозначное число;
• примеры на нахождение сторон, периметра и площади квадрата и прямоугольника;
• простые задачи на движение: нахождение скорости, времени или расстояния.

Программа «Задание на неделю 3 класс» написана в Excel с помощью макросов. Данные генерируются случайным образом, что позволяет получить более тысячи вариантов заданий для 3 класса, карточки заданий не повторяются.

Для ознакомления с программой можно скачать изображение карточки, которая получилась с помощью программы. Для получения новой карточки математического диктанта достаточно скачать, нажать на кнопку и распечатать.

Другие программы, которые помогут закрепить навыки счета:

• Цепочки примеров в пределах 1000 (все действия)
• Числовые пирамиды большие (в пределах 50,100 и больше)
• Умножение и деление по типам (табличное, внетабличное, круглых чисел)
• Сложение и вычитание в столбик
• Умножение и деление в столбик
• Деление с остатком на число (с выбором уровня сложности)
• Порядок действий в пределах 1000 (все действия)
• Сложные примеры на порядок действий
• Выражения с именованными числами

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Как решаем:

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

2 + 3 = 5.

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Как лучше запоминать таблицу

Таблицу умножения на уроках по математике 2 класс учит наизусть. Умножение на 2, 3 и так до 5 запоминается легко, не вызывает трудностей у учеников. Гораздо сложнее запомнить ответы таблицы умножения на 8, 7.

Помогут быстрее решать примеры некоторые правила умножения:

• чтобы одно число умножить на другое, нужно первое число сложить с себе подобным столько раз, сколько указывает второе число;
• любое число, умноженное на 1, даст в результате первоначальное число;
• любое число, умноженное на 0, даст в результате 0;
• каждое последующее значение в таблице умножения отличается от предыдущего на исходную цифру (в таблице умножения на 5 разница между последующими числами составит 5, в таблице на 6 – 6 и так далее).

Для облегчения запоминания таблицы умножения используют разные приемы:

• с помощью стихов (рифма поможет запомнить ответы);
• в игровой форме с помощью пальцев, картинок;
• ассоциативная таблица умножения.

Такой способ хорош, если у ребенка хорошо развита зрительная память. Тогда, услышав и увидев зрительный образ примера у него в памяти будет возникать и зрительный образ ответа.

Запомнить таблицу умножения на 9 можно таким образом: показать ребенку закономерность:

2 * 9 = 18

3 * 9 = 27

4 * 9 = 36 и так далее.

Обратите внимание: в ответе первая цифра на единицу меньше множителя, а вторую найти легко – в сумме они обе должны давать 9

Эффективный способ запоминания умножения на 9

Составные задачи деления суммы на число и числа на сумму

1. Было 16 больших и 12 маленьких кнопок. Все их поставили на 4 куртки, поровну на каждую. Сколько кнопок ставили на каждую куртку?2. 38 девочек и 42 мальчика. Всех детей рассадили в 2 автобуса поровну. Сколько детей в каждом автобусе?3. С одного куста облепихи собрали 12 кг ягод, а с другого куста 16 кг. Все ягоды разложили в 4 одинаковых ящика. Сколько килограммов ягод в каждом?4. Коля с одной грядки выдернул 16 морковок, а с другой 24 морковки. Всю морковку он раздал восьми кроликам поровну. Сколько морковок получил каждый?5. С одной пасеки собрали 12 кг мёда, а с другой 9 кг. Весь мёд поровну разлили в 3 бидона. Сколько килограммов мёда в каждом бидоне?6. У Максима было 2 конструктора. В одном конструкторе 60 деталей, а в другом 20 деталей. Из всех деталей он сделал 4 одинаковые машины. Сколько деталей расходовал Максим на каждую машину?7. Для уроков труда купили 16 листов цветного картона и 34 листа простого картона. Весь картон разложили в 5 одинаковых пачек. Сколько листов картона в каждой пачке?8. У дяди Лёши было 15 жёлтых канареек и 5 оранжевых. Всех птиц он разместил в 10 одинаковых клеток. Сколько птиц в каждой клетке?9. Хозяйка утром надоила 16 л молока, а днём 14 л. Всё молоко она разлила в 10 одинаковых банок для продажи. Сколько литров молока в каждой банке?10. Зоопарк получил 19 кг филе хека и 23 кг филе окуня. Всего этого рыбного филе хватило моржонку на 7 дней. Сколько килограммов рыбного филе получает моржонок в день, если ежедневно ему выдают одинаковое количество филе?

Карточка 2

Сосчитай, записывая примеры в столбик.

32+49	37-16
46+24	70-48
83+8	53-38
38+32	45-8

Сосчитай, записывая примеры в столбик.

80-67	45+14
93-48	38+47
59-42	75+8
36-9	68+27

Сосчитай, записывая примеры в столбик.

46+37	80-38
22+58	93-56
59+9	75-9
64+27	87-32

Карточка 7

В летний лагерь приехали дети на двух автобусах. В первом автобусе было 46 детей, а во втором — на 8 детей меньше. Сколько всего детей приехало в школьный лагерь?

3∙7	2∙9	5∙3	9∙0
20:4	70:10	8∙10	32:4
27:3	21:7	7∙4	8∙3

c∙4=12

6∙c=18

27:c=3

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

70-(7∙3)+(8∙4)

Найди значение выражения, решая по действиям.

64-(27+14)+(6∙4)

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

38+(6∙3)-(4∙7)

Карточка 20

На зиму мама закрыла 4 банки вишнёвого варенья, а малинового — в 3 раза больше. Сколько банок малинового варенья закрыла мама? Сколько всего банок закрыла мама на зиму?

Карточка 21

В первый день маляр покрасил 5 скамеек, а во второй — в 4 раза больше. Сколько скамеек покрасил маляр во второй день? Сколько всего скамеек покрасил маляр за два дня?

Карточка 22

Пятачок за неделю съел 3 баночки мёда, в Винни-Пух — в 3 раза больше. Сколько баночек мёда съел Винни-Пух? Сколько баночек мёда они съели вместе?

Карточка 23

Перед домом посадили 4 ели, а берёз — в 3 раза больше. Сколько посадили берёз? Сколько всего деревьев посадили перед домом?

Карточка 24

Денис нарисовал 16 флажков, а Дима — в 4 раза меньше. Сколько флажков нарисовал Дима? Сколько всего флажков нарисовали мальчики?

Карточка 25

Алёна придумала 12 загадок, а Максим — в 2 раза меньше. Сколько загадок придумал Максим? Сколько всего загадок придумали оба мальчика?

Карточка 26

Мастер за день изготовил 24 детали, а его ученик — в 3 раза меньше. Сколько деталей изготовил ученик? Сколько всего деталей они изготовили вместе?

Карточка 28

На первом острове живёт 32 индейца, а на втором — в 4 раза меньше. Сколько индейцев живёт на втором острове? Сколько всего индейцев на двух островах?

Карточка 29

В куске было 54 метра ткани. Из этой ткани сшили 8 курток, расходуя по 3 метра на каждую. Сколько метров ткани осталось в куске?

В театре ученики первого класса заняли в партере 2 ряда по 9 мест и еще 13 мест в амфитеатре. Сколько всего мест заняли ученики первого класса?

Актовый зал освещает 6 люстр по 8 лампочек в каждой, да еще 7 лам­почек над сценой. Сколько всего лампочек освещает актовый зал?

К празднику купили 4 набора шариков по 10 штук в каждом наборе. Лопнули 12 шариков. Сколько шариков осталось на празднике?

В 3 одинаковых наборах 18 карандашей. Сколько карандашей будет в 7 таких наборах?

Начерти таблицу и реши задачу.

Для изготовления 5 одинаковых конструкторов потребовалось 35 деталей. Сколько деталей нужно для изготовления 8 таких конструкторов?

Начерти таблицу и реши задачу.

Крупу разложили на 6 одинаковых упаковок общей массой 12 кг. Сколько упаковок получится из 20 кг?

Начерти таблицу и реши задачу.

В 3 банки для засолки разложили 12 кг помидоров. Сколько банок потребуется для засолки 32 кг помидоров?

Начерти таблицу и реши задачу.

На 32р. купили 4 тетради. Сколько тетрадей можно купить на 56 рублей? на 16 рублей?

Начерти таблицу и реши задачу.

В 2 ведра помещается 16 кг картофеля. Сколько вёдер нужно, чтобы разложить 24 кг картофеля?

Начерти таблицу и реши задачу.

В 4 наборах 32 листа цветной бумаги. Сколько наборов составляют 72 листа бумаги?

Начерти таблицу и реши задачу.

• Начерти прямоугольник со сторонами 8 см и 4 см. Найди его площадь и периметр.
• Сравни:

12 смc1см2мм	7 мc74 дм	9 ммc1 см
14 смc1дм4см	8см7ммc90 мм	100 смc1 м

• Начерти прямоугольник со сторонами 5 см и 4 см. Найди его площадь и периметр.
• Сравни:

14 смc1см4мм	9 мc94 дм	9 ммc1 см
18 смc1дм8см	6см7ммc70 мм	10 смc1 дм

Расставь знаки «+», «-», «·», «: » так, чтобы равенства стали верными.

26*6*7=13	2*2*4=0
7*9*2=18	8*9*2=70
9*9*2=20	8*4*2=30
9*2*2=16	40*5*7=56

Из 12 м ткани портной сшил 6 одинаковых костюмов. Сколько метров ткани потребуется на 10 таких костюмов? на 7 костюмов?

Начерти таблицу и реши задачу.

В огороде собрали 24 кг моркови, редиса — в 4 раза меньше, чем моркови, а чеснока — в 5 раз больше, чем редиса. Сколько килограммов чеснока собрали?

Из 15 м тюля сшили 5 одинаковых занавесок. Сколько таких занавесок можно сшить из 21 м тюля? Сколько понадобится тюля, чтобы сшить 9 таких занавесок?

Начерти таблицу и реши задачу.

Выполнение деления

Между нахождением частного и произведения существует тесная взаимосвязь. Особенно она просматривается при решении примеров на деление в 5 классе. По сути, эти 2 действия являются обратными друг другу. Математическим языком это можно описать как b * a = c → b = c / a. Эта зависимость в дальнейшем довольно сильно помогает решать сложные многозначные уравнения.

Существует несколько способов поиска частного:

1. Последовательное вычитание. Нужно число разделить на другое. Чтобы найти ответ, понадобится из делимого вычитать делитель до тех пор, пока в ответе не получится 0. Затем следует подсчитать количество вычитаний. Это число и будет искомым ответом. На самом деле этот способ используется редко из-за своей громоздкости.
2. Представление в виде произведения. При решении примеров иногда удобно делимое разложить на множители, причём так, чтобы один из них легко можно было разделить на делитель. Например, 560 / 56 = (56 * 10) / 56 = 10.
3. Использование метода «уголок». Это наиболее часто применяемый способ. Делимое с делителем записывают в строчку, разделяя горизонтальной чертой. Вначале, сравнивая цифры, определяют неполное частное. Если в числе, что стоит справа, количество единиц меньше, добавляют следующий разряд. Затем подбирают такой множитель, чтобы при его умножении на делитель ответ не превышал выбранную часть делимого. Полученный результат записывают под низом делителя. Это будет первая цифра частного. Далее, от делимого вычитают результат умножения. Такие действия повторяют до тех пор, пока не получится 0.

Существуют методы, позволяющие проверить, насколько правильно найдено частное. Для этого нужно полученный ответ перемножить с делителем. Например, 12 / 4 = 3. Отсюда 3 * 4 = 12. Все три члена идентичные, значит, ответ найден верно.

Следует знать, что есть приёмы, позволяющие облегчить выполнение действия. При нахождении результата деления, когда нужно найти частное двух одинаковых чисел, в ответе будет единица: 345/ 345 = 78 / 78 = 89976 / 89976 = 1.

Входная административная контрольная работа

1 вариант

1. Выполни вычисления

3 • 8 = 4 • 6 = 9 • 3 = 7 • 4 =

16 : 4 = 28 : 4 = 21 : 3 = 36 : 9 =

20 : 5 = 4 • 8 = 12 : 6 = 3 • 7 =

2. Вычисли

80 + 24 : 6 =

50 – 4 • (12 – 5) =

70 – 5 • 4 =

3. Задача

Упаковщица уложила в коробку 2 ряда синих кубиков, по 8 кубиков в ряду и 12 зелёных кубиков. Сколько всего кубиков было в коробке?

4. Реши уравнение

16 : х = 8                               6 • х = 12

5. Найди периметр прямоугольника, длины сторон которого 8 см и 6 см.

2 вариант

1. Выполни вычисления

3 • 9 = 7 • 3 = 3 • 4 = 4 • 6 =

36 : 4 = 20 : 5 = 18 : 6 = 28 : 7 =

7 • 2 = 8 • 4 = 27 : 9 = 2 • 8 =

2. Вычисли

70 + 5 • (12 – 8) =

12 : 6 + 6 • 3 =

60 + 3 • 8 =

3. Задача

Мама разложила пирожки на 3 маленькие тарелки, по 6 пирожков на каждую, и 10 пирожков на большую тарелку. Сколько всего пирожков на этих тарелках?

4. Реши уравнение

18 : х = 3                               7 • х = 14

5. Найди периметр прямоугольника, длины сторон которого 9 см и 5 см.

Законы умножения

Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.

Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.

Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.

Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.

Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.

Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:

Таким образом, если число 3 повторить два раза подряд, получится число 6.

Переместительный закон умножения

Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:

От перестановки мест сомножителей произведение не меняется.

Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.

3 × 5 = 15

Теперь поменяем местами сомножители:

5 × 3 = 15

В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:

3 × 5 = 5 × 3

15 = 15

А с помощью  переменных переместительный закон умножения можно записать так:

a × b = b × a

где a и b — сомножители

Сочетательный закон умножения

Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:

3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24

Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:

3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24

В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(3 × 2) × 4 = 3 × (2 × 4)

24 = 24

а с помощью переменных сочетательный закон умножения можно записать так:

a × b × c = (a × b) × c = a × (b × c)

где вместо a, b, c могут стоять любые числа.

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.

Например, найдём значение выражения (2 + 3) × 5

Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:

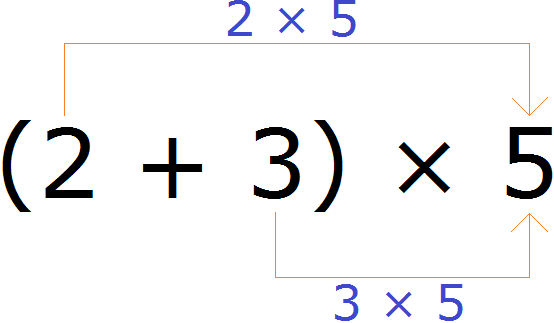
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25

Значит значение выражения (2 + 3) × 5 равно 25.

С помощью переменных распределительный закон умножения записывается так:

(a + b) × c = a × c + b × c

где вместо a, b, c могут стоять любые числа.

Закон умножения на ноль

Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Например, выражение 0 × 2 равно нулю

0 × 2 = 0

В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Ответ — никак.

Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».

И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:

0 × 2 = 2 × 0

0 = 0

Примеры применения закона умножения на ноль:

5 × 0 = 0

5 × 5 × 5 × 0 = 0

2 × 5  × 0 × 9  × 1 = 0

В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.

Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.

Составные задачи на нахождение количества

1. У Игоря 21 руб., у Валеры 14 руб. Сколько фруктового мороженого можно купить, если одно мороженое стоит 7 руб.?2. У Светы 50 руб., а у Люды 30 руб. Сколько пакетов с сухарями они смогут купить, если один пакет стоит 10 руб.?3. У Саши 35 руб., а у Вити 28 руб. Сколько отвёрток они смогут купить, если одна отвёртка стоит 7 руб.?4. У Лены 40 руб., а у Оли 60 руб. Сколько нитей мишуры они могут купить, если одна нить стоит 10 руб.?5. У тёти Тамары 56 руб., а у тёти Люси 24 руб. Сколько пар детских носочков они смогут купить для своих детей, если одна пара стоит 8 руб.?Реши разными способами6. У Вики 40 руб., а у Насти 20 руб. Сколько баночек шоколадной пасты они смогут купить, если одна баночка стоит 10 руб.?7. У Серёжи 18 руб., а у Коли 12 руб. Сколько поплавков могут купить мальчики, если один поплавок стоит 6 руб.?8. У Сюзанны 18 руб., а у Ани 36 руб. Сколько поддонов для цветов могут купить девочки, если один поддон стоит 6 руб.?9. 5 одинаковых тюбиков зубной пасты стоят 50 руб. Сколько таких тюбиков зубной пасты можно купить на 20 руб.?10. 4 упаковки макарон стоят 32 руб. Сколько упаковок макарон можно купить на 56 руб.?

Простые задачи на нахождение количества

1. Одна пара детских носков стоит 8 руб. Мама купила несколько пар и заплатила 72 руб. Сколько пар детских носков купила мама?2. Сколько батареек можно купить на 16 руб., если одна батарейка стоит 4 руб.?3. Тётя Лиля за лук заплатила 24 руб. Сколько килограммов лука она купила, если 1 кг лука стоит 8 руб.?4. 1 пачка конфет «Холодок» стоит 2 руб. Вика потратила на эти конфеты 8 руб. Сколько пачек конфет «Холодок» купила Вика?5. Сколько резинок для волос можно купить на 18 руб., если одна резинка стоит 2 руб.?6. Карандаш стоит 2 руб. Сколько таких карандашей можно купить на 10 руб.?7. Газета стоит 6 руб. Сколько таких газет можно купить на 18 руб.?8. Булавка стоит 3 руб. Сколько таких булавок можно купить на 15 руб.?9. Один стакан молочного коктейля стоит 8 руб. Мальчики взяли несколько стаканов и заплатили 40 руб. Сколько стаканов коктейля взяли мальчики?10. Сколько можно купить цветочных горшков на 54 руб., если один горшок стоит 6 руб.?

Задачи на нахождение периметра

1. Начертите квадрат со стороной 8 см. Чему равен его периметр?2. Длина прямоугольника 5 м, ширина 3 м. Чему равен его периметр?3. Начертите квадрат со стороной 6 см. Чему равен его периметр?4. Длина прямоугольника 6 см, ширина 3 см. Чему равен его периметр? Начертите этот прямоугольник.5. Длина прямоугольника 5 см, ширина 4 см. Чему равен периметр прямоугольника? Начертите этот прямоугольник.6. Длина прямоугольника 5 дм, а ширина на 3 дм короче. Чему равен его периметр?7. Начертите квадрат со стороной 9 см. Чему равен его периметр?8. Длина прямоугольника 8 см, ширина 1 см. Чему равен его периметр? Начертите этот прямоугольник. 9. Сторона квадрата 5 м. Чему равен его периметр? 10. Начертите квадрат со стороной 4 см. Чему равен его периметр?

Общие сведения

Математические вычисления сопровождают человека на всём протяжении его жизни. Когда произносится слово «число», имеется в виду определённый символ, определяющий количество чего-либо. Существуют различного вида выражения, например, целые, дробные, логарифмические. Но самыми простыми являются натуральные. Своё название они получили из-за применения в повседневной жизни. Их используют для счёта и определения порядка.

Таким образом, под натуральными числами понимают выражения, применяемые для определения количества любого физического объекта или присваивания порядкового номера. Например, 3, 1789, 9876, 100009. Если такие числа расположить в порядке увеличения, этот ряд называют натуральным. Последовательность 2, 3, 4, 5 будет именно такой. Нужно отметить, что натуральный ряд бесконечен, наибольшего значения в нём не существует.

Есть несколько систем счисления. В зависимости от неё, для обозначения используется различный набор символов. В России, США, европейских странах применяют арабскую систему. При этом в повседневности используется десятичная разрядность, то есть для записи чисел берут знаки от 0 до 9.

С числами можно выполнять любые действия. Их складывают, вычитают, перемножают и делят. Кроме этого, возводят в степень, извлекают из-под корня, логарифмируют и дифференцируют.

К основным свойствам натуральных чисел относят:

• коммутативность при прибавлении;
• бинарность операции умножения;
• ассоциативность при сложении и умножении;
• дистрибутивность произведения относительно сложения.

Эти свойства важны. На них часто опираются при решении примеров на умножение и деление в 5 классе средней школы. Каждая запись числа состоит из определённого количества разрядов. По сути, она составляет совокупность разрядных слагаемых. В качестве единиц принимают десятки. Любое натуральное выражение можно представить в виде суммы таких чисел. Например, 89 состоит из 8 десятков и 9 единиц. Значит, равенство 89 = 80 + 9 будет справедливым.

Неизвестную натуральную цифру принято обозначать маленькой латинской буквой эн (n). Интересно то, что пересчитать все числа невозможно.

Простые задачи деления по содержанию

1. 18 кг вишнёвого варенья разлили в банки по 3 л в каждую. Сколько понадобилось банок?2. 24 ломтика сала разложили на хлеб по 3 ломтика на каждый кусок хлеба. Сколько потребовалось кусков хлеба?3. 8 хомяков посадили в клетки по 2 хомяка в каждую клетку. Сколько клеток занято хомяками?4. 15 тетрадей разложили в папки по 3 в каждую. Сколько получилось папок?5. 8 самолётов стояли в ангарах по 4 в каждом. Сколько ангаров заняли самолёты?6. Мама испекла 24 пирожка. На каждом противне она пекла по 6 пирожков. Сколько противней с пирожками испекла мама? 7. 24 мяча разложили в коробки по 6 мячей в каждую. Сколько коробок с мячами получилось?8. 70 кг сена выдали коровам по 7 кг каждой. Сколько коров получили сено?9. На стройку привезли 24 т песка. Сколько машин привезли этот песок, если на каждой машине привезли по 8 т песка?10. 50 лампочек зажглось в гирляндах по 10 лампочек в каждой. Сколько новогодних гирлянд зажглось?