Многофункциональный решебник по математике

В каких случаях перед «как» ставится запятая

Ответ на этот вопрос зависит от конкретного случая. «Точка с хвостиком» может располагаться в препозиции к лексеме «как», если:

• в центральной части предложения или ближе к его концу имеются выражения, выступающие как вводные (их также называют сравнительными оборотами): как всегда, как правило, как исключение, как следствие, как нарочно, как теперь, как сейчас; «как» входит в состав данных сочетаний и обособляется вместе с ними (имейте в виду, что бывают ситуации, когда данные конструкции находятся в тесной связи со сказуемым и запятой не выделяются);
• союз находится в составе выражений «не что иное как», «не кто иной как»;
• союз соединяет части сложноподчиненного предложения: главная часть находится впереди, за ней следует придаточное, которое начинается с «как»;
• имеется сравнительный оборот, где обстоятельство начинается с данного союза. Сравнение выступает в качестве уподобления одного предмета другому, одной ситуации – другой. Исследователи отмечают три основных компонента, составляющих ядро данного понятия. Во-первых, объект сравнения – то, что сравнивается; во-вторых, субъект сравнения – то, с чем сравнивается, и, в-третьих, основание сравнения, или связующий признак.
• имеются сравнительные обороты, содержащие оттенок причинности, начинающиеся с «как и»;
• до сравнения присутствуют лексемы «так, тот, такой, столь».
• в предложении есть сравнительные конструкции «как и прежде», «как и раньше», «как прежде», «как раньше».

Примеры предложений

Когда я только собралась выходить, как нарочно, начался дождь (в центре синтаксической конструкции имеется сочетание «как нарочно», выделяющееся запятыми с обеих сторон).

Учащиеся прекрасно знают, как выполняется морфологический разбор существительного (в препозиции по отношению к главному находится придаточное изъяснительное, начинающееся с «как»).

Я точно купил газету, как ты и просил (союз находится в придаточной части СП).

Пусть все будут веселы, не завистливы и не ссорятся друг с другом, как злые собаки (содержится полное сравнение: объект сравнения – все, субъект сравнения – злые собаки, основание сравнения – ссорятся; «как» располагается перед субъектом сравнения).

Алексей, как юноша честный и порядочный, признался, что забыл предупредить одногруппников о предстоящем семинаре (сравнительный оборот «как юноша честный и порядочный» имеет оттенок причинности).

В современном мире нечасто можно встретить такого добродушного человека, как он (имеется «такого», поэтому перед союзом есть запятая).

В Москве, как и во всей стране, недавно прошли выборы (оборот начинается с «как и»).

Мне почудилось, что за калиткой за мной наблюдает не кто иной, как Саша (в конструкции «не кто иной, как»).

Вы будете счастливы, как и прежде (конструкция «как и прежде» обособляется).

Давайте будем жить тихо, мирно, как и раньше (оборот «как и раньше» обособляется).

Формула полной вероятности и формула Байеса

Если событие А может произойти только при выполнении одного из событий B₁, B₂, …, B_n, которые образуют полную группу несовместных событий — вероятность события А вычисляется по формуле полной вероятности:

Вновь рассмотрим полную группу несовместных событий B₁, B₂, …, B_n, вероятности появления которых P(B₁), P(B₂), …, P(B_n). Событие А может произойти только вместе с каким-либо из событий B₁, B₂, …, B_n, которые называются гипотезами. Тогда по формуле полной вероятности: если событие А произошло — это может изменить вероятности гипотез P(B₁), P(B₂), …, P(B_n).

По теореме умножения вероятностей:

откуда

Аналогично, для остальных гипотез:

Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.

Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Как рассуждаем:

1. Возможны три гипотезы:
   • А1 — на линию огня вызван первый стрелок,
   • А2 — на линию огня вызван второй стрелок,
   • А3 — на линию огня вызван третий стрелок.
2. Так как вызов на линию огня любого стрелка равно возможен, то
3. В результате опыта наблюдалось событие В — после произведенных выстрелов мишень не поражена. Условные вероятности этого события при наших гипотезах равны:
4. По формуле Байеса находим вероятность гипотезы А₁ после опыта:

Ответ: 0,628.

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

np — q ≤ k ≤ np + p, где q=1−p

Так как np−q = np + p−1, то эти границы отличаются на 1. Поэтому k, являющееся целым числом, может принимать либо одно значение, когда np целое число (k = np), то есть когда np + p (а отсюда и np — q) нецелое число, либо два значения, когда np — q целое число.

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

Как решаем:

1. По условию дано: n = 730, p = 1/365, g = 364/365
2. np — g = 366/365
3. np + p = 731/365
4. 366/365 ≤ m ≤ 731/365
5. m = 2

Ответ: 2.

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

• 0,600 = 0,6
• 21,10200000 = 21,102

Основные свойства
Дробь не имеет значения, при условии, если делитель равен нулю. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет. Две дроби a/b и c/d называются равными, если a * d = b * c. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Как решать квадратные уравнения через дискриминант

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения

Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней

Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax2 + bx + c = 0:

• как найти дискрининант: D = b2 − 4ac;
• если дискриминант отрицательный — зафиксировать, что действительных корней нет;
• если дискриминант равен нулю — вычислить единственный корень уравнения по формуле х = — b2/2a;
• если дискриминант положительный — найти два действительных корня квадратного уравнения по формуле корней

А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2- 4ac = 4n2 — 4ac = 4(n2- ac) и подставим в формулу корней:

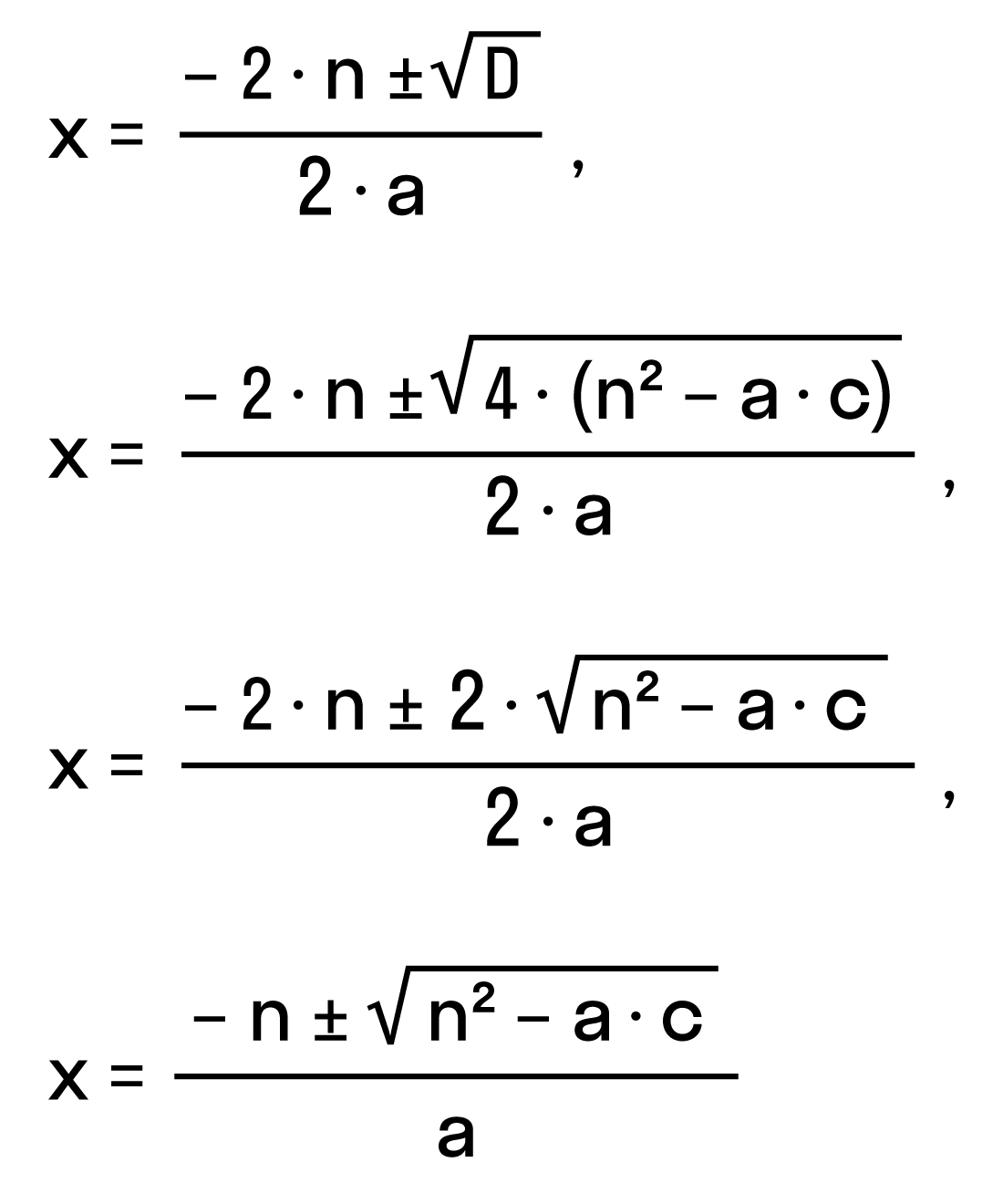
Для удобства вычислений обозначим выражение n2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n2- ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n2- ac;
• если D₁< 0, значит действительных корней нет;
• если D₁= 0, значит можно вычислить единственный корень уравнения по формуле;
• если же D₁> 0, значит можно найти два действительных корня по формуле

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11×2 — 4 x — 6 = 0, чем 1100×2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100×2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12×2- 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2×2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2×2- 3x + 7 = 0 перейти к решению 2×2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

• x₁ + x₂ = — b/a,
• x₁* x₂ = c/a.

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3×2- 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

• Калькулятор раз
• Два
• Три

Действия с десятичными дробями

С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.

Как разделить десятичную дробь на натуральное число

1. Разделить целую часть десятичной дроби на это число.
2. Поставить запятую в частном и продолжить вычисление, как при обычном делении.

Пример 1. Разделить 4,8 на 2.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
3. Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
4. Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:

Ответ: 4,8 : 2 = 2,4.

Пример 2. Разделить 183,06 на 45.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
3. Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
4. Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.

Как разделить десятичную дробь на обыкновенную

Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.

Пример 1. Разделить 0,25 на 3/4.

Как решаем:

1. Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
2. Разделить дробь по правилам:

Ответ: 0,25 : 3/4 = 1/3.

Пример 2. Разделить 2,55 на 1 1/3.

Как решаем:

1. Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
2. Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
3. Разделить дробь по правилам:

Ответ: 2,55 : 1 1/3 = 1 73/80.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить 2/5 на 0,8.

Как решаем:

1. Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
2. Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.

Ответ: 2/5 ∗ 0,8 = 0,32.

Пример 2. Умножить 0,28 на 6 1/4.

Как решаем:

1. Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
2. Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.

Ответ: 0,28 ∗ 6 1/4 = 0,8.

А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

• Калькулятор раз
• Два
• Три

Определение показательного уравнения

Показательными называются уравнения с показательной функцией f(x) = aх. Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: aх = b, где a > 0, a ≠ 1.

• разложение многочлена на множители;
• свойства степенной функции;
• решение квадратных уравнений.

Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.

С точки зрения геометрии показательной функцией называют такую: y = ax, где a > 0 и a ≠ 1

У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a

Это хорошо видно на рисунке ниже.

Важно знать
Показательная функция не может быть отрицательным числом, т. е

выражение у = ax при а ≤ 0 корней не имеет.

Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.

Свойства степеней

Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.

am x an	am+n
am:an	am-n
(a x b)n	an x bn
(a : b)n	an : bn
(an)m	an x m
a-n	1/an
(a/b)-n	(b/a)n
n√a	a1/n

Как видите, ничего нового здесь нет, все это проходят в 6–7 классе.

Как записать десятичную дробь

Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.

Как решаем:

1. Знаменатель равен 10 — это один ноль.
2. Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
3. В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.

Ответ: 16/10 = 1,6.

Пример 2. Перевести 37/1000 в десятичную дробь.

Как решаем:

1. Знаменатель равен 1000 — это три нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Так как в числителе только две цифры, то на пустующие места пишем нули.
4. В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.

Ответ: 37/1000 = 0,037.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Вот, что делать:

1. Найдем наименьшее общее кратное для определения единого делителя.

   Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

   НОК (15, 18) = 3 * 2 * 3 * 5 = 90

2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

   90 : 15 = 6,

   90 : 18 = 5.

   Полученные числа запишем справа сверху над числителем.

3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
   • если делимое больше делителя, нужно преобразовать в смешанное число;
   • если есть что сократить, нужно выполнить сокращение.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

1. Сложить целые части.
2. Сложить дробные части.

   Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

3. Суммировать полученные результаты.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

11 класс

Математика входит в список базовых предметов, которые школьники начинают познавать уже с первого класса. Это точная наука, которая требует усидчивости и полного внимания. Однако в младших классах от учеников еще трудно добиться нужной внимательности и трудолюбия. Но это совсем не означает, что младшеклассники не смогут освоить необходимую математическую базу.

Авторы представленных решебников по математике являются заслуженными педагогами и отличными специалистами своего дела. Они прекрасно знают необходимый подход к ребенку и предоставляют готовые ответы в очень доступной и понятной любому школьнику форме. В данном разделе вы найдете ГДЗ по математике для всех классов (1 и 2,3 и 4, а также 5,6,7,8,9,10 и 11).

Решебники по математике включают полностью проработанные готовые ответы ко всем упражнениям и заданиям из современных школьных учебников. Такие ответы оформляются в соответствии с нумерованными списками их оглавления учебника. Также авторы улучшают свои пособия дополнительными краткими комментариями и необходимыми иллюстрациями, которые помогают гораздо быстрее и качественнее освоить новый материал.

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+)
• вычитание (-)
• умножение (*)
• деление (:)

Операции отношения:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
• 3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.

Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.

Возведение степень — операция умножения числа на самого себя несколько раз.

Основание степени — число, которое повторяется сомножителем определённое количество раз.

Показатель степени — число, которое указывает, сколько раз берется одинаковый множитель.

Степенью называется число, которое получается в результате взаимодействия основания и показателя степени.

• Запись: 34 = 81, где 3 — основание степени, 4 — показатель степени, 81 — степень.
• 3^4 = 3 * 3 * 3 * 3

Вторая степень называется квадратом, третья степень — кубом. Первой степенью числа называют само это число.

Извлечение корня — арифметическое действие, обратное возведению в степень.

• Запись: 4√81 = 3, где 81 — подкоренное число, 4 — показатель корня, 3 — корень.
• З^4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
• 2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = -b : а; если а равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

• кубические
• уравнение четвёртой степени
• иррациональные и рациональные
• системы линейных алгебраических уравнений

Приведение к одинаковой степени

Не все показательные уравнения с разными основаниями можно решить предыдущим способом. Иногда проще преобразовать не основания, а показатели степени. Правда, пользоваться этим методом есть смысл только в том случае, когда мы имеем дело с умножением или делением.

При умножении чисел с разными основаниями, но одинаковыми степенными показателями можно перемножить только основания (степень останется прежней): axbx = (ab)x.

Пример

52х-4 = 492-х

Общих множителей у левой и правой части уравнения нет и привести их к одинаковому основанию достаточно трудно. Поэтому стоит поработать с показателями степеней:

52х-4 = 492-х

52х-4 = 74-2х

52х-4 = (1/7)2х-4

352х-4 = 1

2х — 4 = 0

х = 2

Пример 2

2х-2 = 52-х

Нам нужно привести обе части уравнения к одинаковым степенным показателям, и для этого вначале попробуем преобразовать правую часть, используя свойство степенных функций.

2х-2 = 1/5х-2

Теперь умножим обе части на 52-х и придем к уравнению:

2х-2 × 52-х = 1

10х-2 = 1

10х-2 = 10

х — 2 = 0

х = 2

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax2 + c = 0, при b = 0;
• ax2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.

Уравнение ax2 = 0 равносильно x2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6×2 = 0.

Как решаем:

1. Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

   −6×2 = 0

   x2 = 0

   x = √0

   x = 0

Ответ: 0.

Как решить уравнение ax2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax2 + c = 0:

• перенесем c в правую часть: ax2 = — c,
• разделим обе части на a: x2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.

Если — c/а > 0, то корни уравнения x2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах
Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению ax2 + c = 0, которое: не имеет корней при — c/а < 0; имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.

Пример 1. Найти решение уравнения 8×2 + 5 = 0.

Как решать:

1. Перенесем свободный член в правую часть:

   8×2 = — 5

2. Разделим обе части на 8:

   x2 = — 5/8

3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8×2 + 5 = 0 не имеет корней.

Как решить уравнение ax2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

1. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

2. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:

• x = 0;
• x = −b/a.

Пример 1. Решить уравнение 0,5×2 + 0,125x = 0

Как решать:

1. Вынести х за скобки

   х(0,5x + 0,125) = 0

2. Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
3. Решить линейное уравнение:

   0,5x = 0,125,
   х = 0,125/0,5

4. Разделить:

   х = 0,25

5. Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

В каких случаях запятая перед «как» не нужна

• конструкция с «как» выступает в роли обстоятельства образа действия; ее можно заменить на аналогичное наречие или существительное в творительном падеже;
• «как» находится в составе фразеологического оборота, устойчивого сочетания;
• лексема является именной частью составного сказуемого;
• до сравнительного оборота имеется отрицательная частица «не» или лексемы «совершенно, почти, совсем, вроде, точь-в-точь, прямо, просто, именно»;
• «как» выполняет функцию тире между подлежащим и сказуемым, когда они выражены именительным падежом существительного;
• является частью составных союзов «как…так и», «так как», «с тех пор как», «по мере того как», «с того времени как»;
• «как» входит в состав наречных выражений «как можно скорее», «как можно больше», «как можно меньше», «как можно лучше»;
• имеется сочетание «выглядит как» (в нем сказуемое бессмысленно без следующего существительного, присоединяемого союзом «как»).

Примеры предложений

Снег покрыл землю как мягкий ковер (оборот «как мягкий ковер» – обстоятельство образа действия, его можно поставить в творительном падеже – мягким ковром).

На рассвете трава блестела как изумруд (оборот «как изумруд» – обстоятельство образа действия, можно употребить в творительном падеже – изумрудом).

Бабушка как в воду глядела (в составе фразеологизма не обособляется).

Брат везде и всегда чувствует себя как рыба в воде (в составе фразеологизма не обособляется).

Им надоело жить как кошка с собакой (в составе фразеологизма не обособляется).

Он ведет себя как ребенок (в составе именной части сказуемого).

Многие исследователи говорят о «Судьбе человека» М. Шолохова как о рассказе (в составе именного сказуемого).

Мальчишка рассуждал совсем как взрослый (перед «как» находится лексема «совсем»).

В нашем кругу он был известен совсем не как доктор (до «как» присутствует отрицательная частица «не»).

Он вошел в кабинет уже не как сотрудник (до «как» присутствует отрицательная частица «не», знака препинания не требуется).

Книга как подарок (вместо союза между подлежащим и сказуемым можно поставить тире).

Для офиса были приобретены как канцелярские принадлежности, так и средства бытовой химии (перед первой частью составного союза «как… так и» никогда не ставится запятая).

Сотрудник плотно пообедал, так как ему предстояло сегодня остаться в офисе до позднего вечера («точка с хвостиком» имеется только перед первой частью составного союза «так как»).

Соберите всех присутствующих сотрудников и, как можно скорее, проведите инструктаж по технике безопасности (наречное выражение «как можно скорее» никогда не обособляется).

Уделите этому учащемуся как можно больше внимания (наречное выражение «как можно больше» не обособляется).

Молодой человек выглядит как журналист (конструкция «выглядит как» не обособляется).

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

1. преобразовать смешанные дроби в неправильные;
2. перемножить числители и знаменатели дробей;
3. сократить полученную дробь;
4. если получилась неправильная дробь, преобразовать в смешанную.

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

• числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
• знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше. Для деления смешанных чисел необходимо:

Для деления смешанных чисел необходимо:

• представить числа в виде неправильных дробей;
• разделить то, что получилось друг на друга.

Определение простого предложения

Мы уже знаем, какое предложение является простым — то, у которого всего одна грамматическая основа.

Примеры простых предложений:

• Мы ездили на машине (одна грамматическая основа: мы ездили).

• Я уехал к другу в другой город (одна грамматическая основа: я уехал).

• Он распахнул окно и увидел птицу (одна грамматическая основа с однородными сказуемыми: он распахнул и увидел).

По наличию главного члена — подлежащего или сказуемого — они делятся на:

• Двусоставные, то есть в их составе подлежащее и сказуемое.

• Односоставные, то есть имеют в составе или подлежащее, или сказуемое.

Односоставные конструкции делятся на:

1. Определённо-личные предложения — это односоставные предложения с главным членом сказуемым, которое выражено личной формой глагола в форме 1 или 2 лица или глаголом в повелительном наклонении.

2. Неопределённо-личные предложения — это односоставные предложения с главным членом сказуемым, которое выражено глаголом в форме 3 лица множественного числа в настоящем или будущем времени или в форме множественного числа в прошедшем времени. Если лицо не определено — действие совершается кем-то неопределённым.

3. Обобщённо-личные предложения — это односоставные предложения с главным членом сказуемым, которое стоит в форме 2 лица единственного числа или 3 лица множественного числа в настоящем или будущем времен либо в форме 2 лица единственного или множественного числа повелительного наклонения.

4. Безличные предложения — это односоставные предложения с главным членом сказуемым, которое стоит в форме 3 лица единственного числа настоящего или будущего времени или в форме среднего рода прошедшего времени.

Примеры односоставных предложений:

• Лето!

• Приходи сегодня в спортзал (определенно-личное).

• Его взяли на должность (неопределенно-личное).

• Стало моросить (безличное).

Примеры двусоставных предложений:

• Я пришла поздно с учебы.

• Выстрелил фейерверк.

• Очень странная история произошла со мной сегодня утром.

Кроме главных членов предложения есть еще второстепенные:

• Дополнение отвечает на вопросы косвенных падежей и обозначает предмет.

• Определение обозначает признак предмета и отвечает на вопросы: какой, чей.

• Обстоятельство обозначает признак действия или другого признака.

Виды простых предложений по наличию второстепенных членов:

• Если в предложении есть хотя бы один второстепенный член, оно называется распространенным.

• Если в предложении второстепенных членов нет, а есть только грамматическая основа, оно считается нераспространенным.

По наличию членов, которые влияют на понимание смысла, простые предложения можно разделить на полные и неполные.

Характеристики полных предложений:

• Если в предложении есть все необходимые для понимания компоненты.

• Если для того, чтобы понять смысл предложения, не нужно обращаться к другим предложениям.

Примеры полных предложений:

• Я не боюсь привидений.

• Она не хочет в школу.

Характеристики неполных предложений:

• Если для понимания предложения не хватает компонентов.

• Если, чтобы понять его смысл, нам нужно обратиться к соседним предложениям.

В неполном предложении могут отсутствовать все главные члены, а также второстепенные члены.

Примеры неполных предложений: