Как делить в столбик? как объяснить ребенку деление столбиком? деление на однозначное, двузначное, трехзначное число, деление с остатком

Как научиться делить столбиком 4 класс

Программа 4 класса, по сравнению с прошлым учебным годом, усложняется в сторону увеличения расчетных чисел. Четвероклассники проводят деление многозначных чисел больше 100. Они учатся делить уголком числа с двух и трехзначным делителем, а также решать примеры с остатком.
Алгоритм решения деления уголком аналогичен алгоритму, изучаемому в третьем классе.

Давайте, в качестве примера 1072 разделим на 8. Сразу необходимо определиться с категориями деления, 1072 — делимое, 8 – делитель. Результат, полученный в качестве действия, — частное.
Числа запишем с двух сторон уголка.
Сразу определимся с числом, которое больше самого делителя. 1<8, поэтому начинают действие с 10. В данном числе может содержаться лишь одна 8. Запишем результат в правой колонке.

Делитель 8 умножим на  1 и получим —  8. Результат подпишем под делимым 1072 и вычтем. Полученное число 2<8, поэтому его увеличим за счет следующего неиспользованного числа делимого — 7. В итоге получится цифра «27».
Затем действуют по алгоритму. Проанализируем, сколько восьмерок содержит число «27». В нем заключено 3 х 8=24. Цифру «3» допишем в правой колонке рядом с частным 1. На данный момент частное – 13.
Слева от 27 – 24 = 3.

Деление в столбик на двузначное число

Деление в столбик школьники проходят еще в младших классах на уроках математики. В дальнейшем его применяют как вспомогательное средство при решении задач. Но если не пройти в нормальном виде деление уголков, то могут возникнуть затруднения и с трехзначными числами.

Рис. 1

На рисунке 1 показан принцип деления и названия основных элементов процесса. Как и при делении на однозначные числа, работает алгоритм перехода от крупных к мелким единицам.

Порядок действий опишем, взяв для примера вычисление, представленное на рисунке 1:

1. Выделить самое маленькое двузначное число 63, которое можно поделить на делитель 61. Оно всегда больше того, которое является делителем.

2. Делим 63 на 61. Сколько раз 61 поместится в 63? Один. Записываем под уголком единицу. Это первая цифра частного.

3. Умножаем делитель на эту первую цифру: 61 * 1 = 61, вычитаем из 63 число 61, проводим черту и пишем разность — 2.

4. Сносим следующую цифру делимого — 4. Получаем число 24. Оно не делится на 61, потому записываем ноль на место второй цифры частного (это место рядом с цифрой 1 в нашем примере).

5. Сносим следующую (последнюю в нашем примере) цифру, это 4. Получаем число 244. Делим его на 61. Применим правило устного деления, описанное выше. Нужно подобрать такую цифру, которая при умножении на последнюю цифру (у 61 последняя цифра 1) даст ответ, оканчивающийся на последнюю цифру делимого (у 244 последняя цифра 4, она нам и нужна). Т. е. 4 * 1 = 4. Проверка: 61 * 4 = 244. Мы подобрали цифру 4 и она нам подошла.

6. Вписываем 4 третьей цифрой частного в уголок, получаем 104. Умножаем 61 на 4 и вычитаем результат из 244. Получаем 0. Деление выполнено.

В данном примере делимое — трёхзначное число. В общем случае процесс сноса цифр делимого и деления их на делитель продолжается до тех пор, пока не закончатся все цифры делимого. Этот принцип подходит для трехзначных, четырехзначных и других многозначных чисел.

Как научиться делить столбиком трехзначные числа

Когда в делителе стоит трехзначное число, действие лучше всего выполнять в столбик. Алгоритм математического решения аналогичен делению на двузначное число.

Для примера рассмотрим следующие действия: 146676 : 719

146<719, поэтому сразу возьмем четырехзначное число «1466». В данном значении помещается 2 делителя: 719 х 2= 1438. Цифра «2» будет первым значением частного. Ее запишем справа под уголком.

1466 — 1438 = 28. Полученную разность запишем под чертой слева. Снесем к 28 цифру «7». 287<719, поэтому рядом с двойкой запишем «0».

Снесем последнюю цифру делимого «6», в итоге получится число «2876», которое разделим на 719. Возьмем по 3: 719 х 3 = 2157 — мало, можно взять по 4: 719 х 4 = 2876. Цифру «4» запишем рядом с «20», получим в ответе 204. От 2876 отнимем 2876 , получим разность 0.

Алгоритм деления трёхзначного числа на однозначное

Просмотр содержимого документа
«Алгоритм деления трёхзначного числа на однозначное»

Алгоритм деления трёхзначного числа на однозначное

Я собрал 536 грибов.

По сколько грибов я могу съедать в месяц,

чтобы грибов хватило на 4 месяца?

Ребята, помогите мне

ответить на вопрос!

3

6

:4

5

А можно число

536

зарисовать

графически?

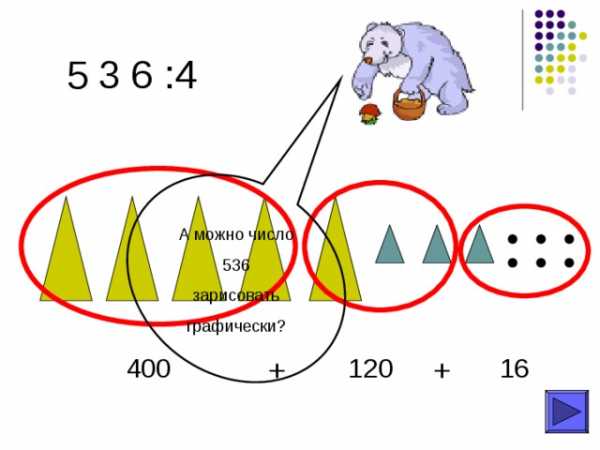
Как число 536 разбить на сумму удобных слагаемых, каждое из которых будет делиться на 4.

+

+

16

120

400

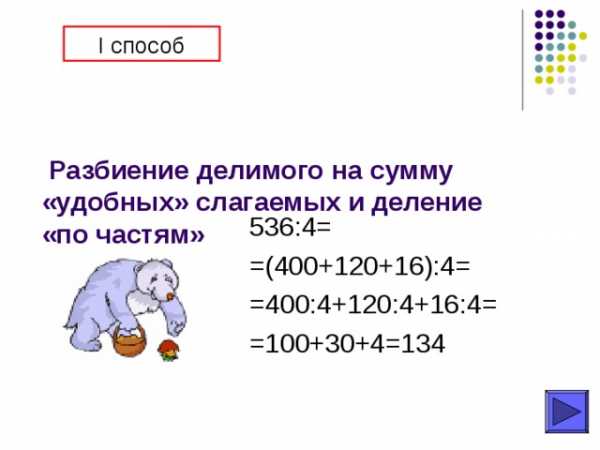
I способ

Разбиение делимого на сумму «удобных» слагаемых и деление «по частям»

536:4=

=(400+120+16):4=

=400:4+120:4+16:4=

=100+30+4=134

II способ

Деление с остатком крупных счётных единиц и последовательный переход к делению более мелких

536:4

• 5 с.:4=1с.(ост.1с.)
• 13д.:4=3д.(ост.1д.)
• 16ед.:4=4ед.

Итак, 534:4=134

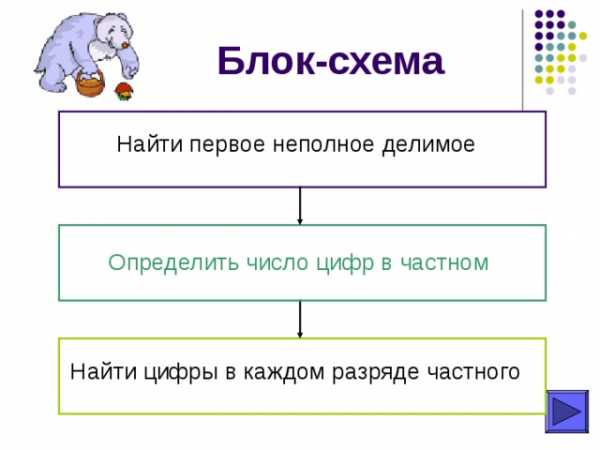
Блок-схема

Найти первое неполное делимое

Определить число цифр в частном

Найти цифры в каждом разряде частного

Первое неполное делимое

4

534

Нахожу первое неполное делимое –

5 сотен

Определение числа цифр в частном

4

534

Первое неполное делимое –

5 сотен

Значит, в частном будет

3 цифры

Нахождение цифр частного

Делим сотни

4

536

4

5 сотен делим на 4

1

1

Берём по 1

1*4=4

Находим остаток

5-4=1

Остаётся 1 сотня

Нахождение цифр частного

Делим десятки

4

536

1 сотня=10 десятков

4

3

1

1

3

10 десятков+3 десятка =

=13 десятков

12

1

13 десятков:4

Берём по 3

3*4=12

Находим остаток

13-12=1

Остаётся 1 десяток

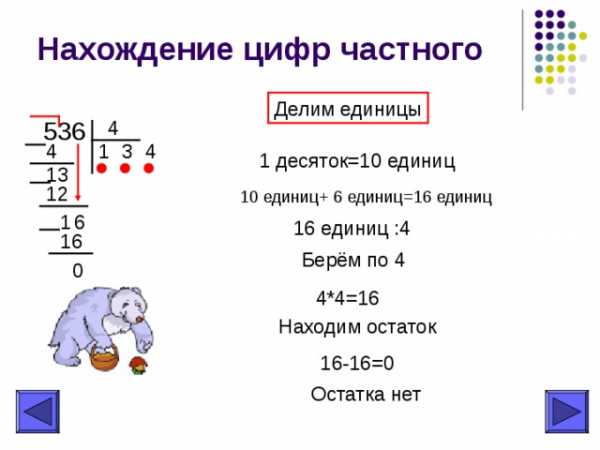
Нахождение цифр частного

Делим единицы

4

536

4

4

3

1

1 десяток=10 единиц

13

12

10 единиц+ 6 единиц=16 единиц

1

6

16 единиц :4

16

Берём по 4

4*4=16

Находим остаток

16-16=0

Остатка нет

Спасибо, ребята!

Ведь я ещё научился делить

трёхзначное число

на однозначное.

До встречи!

Итак, 536:4=134.

Значит, мне можно съедать

по 134 гриба в месяц.

Завершить показ

Правила деления в столбик

Без остатка

Чтобы найти частное от деления одного числа на другое (с любым количеством разрядов) можно выполнить это арифметическое действие в столбик.

Рассмотрим правила деления на практическом примере для лучшего понимания. Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:

1. Пишем делимое (256), затем немного отступаем от него и в этой же строке дописываем делитель (8). Затем между этими числами дорисовываем уголок. Результат будем записывать под делителем.

2. В делимом слева направо отсчитываем минимально необходимое количество разрядов таким образом, чтобы полученное из содержащихся в них цифр новое число было больше, чем делитель. В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.

Примечание: Если крайняя левая цифра делимого больше делителя, добавлять к нему цифру следующего разряда не нужно, и мы сразу приступаем к следующему шагу.

3. Определяем, сколько целых раз наш делитель содержится в полученном из цифр делимого числе (25). В нашем случае – три раза. Пишем цифру 3 в отведенном для этого месте, затем умножаем ее на делитель (3 ⋅ 8). Получившееся число (24) отнимаем из 25 и остается единица

Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления

Примечание: Правила и примеры вычитания чисел столбиком приведены в отдельной публикации.

4. К остатку (1) добавляем следующую цифру делимого (6), чтобы получить новое число, которое снова больше, чем делитель.

Примечание: Если при добавлении следующей цифры образовавшееся новое число все еще меньше делителя, берем еще одну цифру справа (если есть такая возможность), при этом в частном пишем ноль. В противном случае, получается деление с остатком, которое мы рассмотрим далее.

5. В числе 16 содержится ровно два раза по восемь (2 ⋅ 8), следовательно, пишем 2 в частном, затем выполняем вычитание (16 – 16) и получаем остаток, равный нулю.

На этом деление столбиком числа 256 на 8 успешно выполнено, и частное равно 32.

С остатком

В целом, алгоритм действий аналогичен вышеописанному. Разница лишь в том, что при последнем вычитании остается неделимой остаток, к которому больше нечего дописывать из делимого, т.к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.

Например, остаток от деления 112 на 5 равняется двум. То есть 112 : 5 = 22 (2).

Пояснение: в результате вычитания 10 из 12 получается 2, но к нему больше нечего дописать из делимого.

Деление в столбик двузначных, трехзначных, многозначных чисел, чисел с нулями

Не нужно пугаться сразу, что процесс деления не простой, поэтому вы не освоите его. Освоите! В математике следует соблюдать четкие правила, тогда у вас все получится. Алгоритм деления лучше учить на конкретных примерах, ниже будет представлено множество примеров.

Пример деления на трехзначный делитель

Все они выполняются по схеме:

1. Вначале записывается делимое, рядом ставится значок разделить: Ι—, и над чертой пишется делитель (число, на которое делят делимое).
2. Потом необходимо выделить часть делимого для осуществления деления, если это необходимо в данном случае.
3. Далее придется выполнять умножение для того, чтобы определить, сколько раз взять делитель, чтобы получилась выделенная часть делимого. Причем число не должно быть больше 9-ти.
4. Выполняете умножение делителя, записываете результат под делимым, а число ≤ 9-ти записываете под черту знака: Ι– разделить.
5. Из выбранной части делимого вычитаете результат, записываете его под подчеркиванием, сносите следующую цифру делимого, повторяйте опять процесс умножения, пока не разделите число на число.

Рассмотрим деление в столбик на простом примере:

Если такие двухзначные числа, как 16, 28 можно разделить в уме на 2 или 4 (в первом случае при делении на 2 получится 8 и 14), а во втором (4 и 7), то 51 разделить на 3 без столбика уже сложнее. Как происходит деление в столбик распишем на примере 51 разделить на 3.

Деление в столбик

• Как записывается делимое, делитель уже было сказано, визуально можно посмотреть выше на изображении. Делимое идет первым, потом ставится значок деления и над чертой пишут делитель.
• Теперь определяемся, сколько выделить цифр, чтобы начать подбирать множитель, который записывается под чертой в выделенный квадратик на изображении.
• Выделяем одну цифру 5-ку, она больше 3-ки, на черновике распишите примерно какой подобрать множитель, для того чтобы получить число ≤ 5, наглядно это выглядит так: 5 ≥ 3 · 1, число 1 и есть множитель. Его пишут под чертой делить в квадратике.
• Далее под пятеркой пишем произведение 3 · 1 = 3.
• Теперь вычитаем из 5 — 3 = 2. Разница, в нашем случае 2 должна быть < делителя, в нашем случае 3.
• Итак, остается разделить 21 на 3. Из таблицы умножения вы знаете, что: 21 : 3 = 7.
• Семерку пишут под чертой значка делить после единицы. Ответ получается 17.

Далее рассмотрим пример деления трехзначных чисел:

Давайте разделим трехзначное число 512 на 16. Деление будет происходить по той же схеме, что и двухзначного числа.

Пример деления трехзначного числа

• Запишите делимое, делитель, как на фото выше.
• Далее выделим число 51, и узнайте, сколько раз нужно взять число 16, чтобы получилось произведение меньше или равно 51. Итак, выше представлены расчеты: 16 · 3 = 48 < 51.
• Значит под чертой напишите 3, а под делимым 48. Теперь из 51 вычтите 48, получится 3, сносим следующую цифру 2.
• Подберите множитель к 16, чтобы произведение получилось равное или меньше 32. Итого: 16 · 2 = 32.
• Двойку запишите под черту знака деления, а результат 32 под делимым. Итого 32 — 32 = 0.
• Результат 32.

Рассмотрим деление многозначного числа:

Давайте найдем частное 998190 на 135, пример представлен на изображении ниже. Чтобы решить его, следует подставить нужные числа в пустых клетках.

Пример деления в столбик

• Итак, нужно найти первую цифру, на которое нужно умножить число 135, чтобы получить результат ≤ 998. Для этого понадобится знать отлично таблицу умножения и умение складывать цифры. 135 · 7 = 945.
• Число 945 пишите под делимым, вычтите из 998 — 945 = 53. Это число меньше 135, потому нужно снести еще одну цифру 1, получится 531.
• Высчитываем, какой множитель подойдет, к 135, чтобы получить число меньше, чем 534. Решение: 135 · 3 = 405.
• Вторая цифра под чертой знака деления 3, из 531 — 405 = 126.
• Сносим 9, выходит 1269, подбираем множитель к 135. Результат 135 · 9 = 1215.
• Третья цифра под чертой 9. Теперь: 1269 — 1215 = 54.
• Сносим 0, выходит 540, а 540 = 135 · 4, итого последняя цифра результата это 4.
• Результат 7394.

Деление чисел с нулями:

Как научиться делить столбиком 3 класс

Арифметические расчеты в 3 классе базируются на таблице умножения от 1 до 10 в пределах чисел до 100. На этом этапе ребенок должен понимать сам процесс деления и безошибочно определять категории «делителя», «делимого» и «частного». Конечно, деление многозначных чисел проще всего проводить столбиком. Школьник меньше путается и не теряет цифры. Таким образом, вырабатывается мысленная логическая схема. Суть метода нельзя уловить без знания таблицы умножения и способа «обратного» деления.

Алгоритм деления в столбик:

Например, 98 необходимо разделить в столбик на 7.

В нашем примере 98 – делимое, 7 – делитель, результат деления, который получится в итоге – частное. Его и необходимо найти.

Делимое и делитель запишем рядом, разделив их вертикальной линией с уголком. Теперь необходимо определить, сколько семерок поместится в девятке – одна. Цифру «1» запишем под линией в правом нижнем углу.

Под девяткой запишем семерку, подчеркнем линией, отнимем и запишем разницу — 2. Если в двойке не помещается ни одной семерки, значит решение верно. Снесем к двойке верхнюю восьмерку. Получим — 28. Проанализируем, сколько семерок может поместиться в цифре «28» – 4. Полученный ответ запишем рядом с «1».

От 28 отнимем цифру «28» и получим «0» — значит, деление произвели правильно. Если в итоге деления не получается ноль, возможна в подсчетах арифметическая ошибка или деление без остатка невозможно. В итоге частное получилось «14».

Правильность деление можно проверить, если при умножении 14 на 7 получается 98 — подсчеты верны.

Главная проблема, с которой сталкиваются третьеклассники на уроках математики – это отсутствие умения производить быстрые арифметические действия. А ведь вся школьная программа начальной школы базируется на этой основе, особенно действия на деление.

Дьякова Наталия Николаевна: Алгоритмы деления

Первый алгоритм письменного деления
трёхзначного числа на однозначноеДля того чтобы трёхзначное число 684 разделить
на однозначное число 2, надо:

1.Разделить 6 сот. на 2
= 3 сот.

Проверить: 3х2=6. Остатка нет. В частном на месте сотен написать 3.2.Разделить 8 дес. : 2
= 4 дес. Проверить: 4х2=8. Остатка нет. В частном на месте десятков написать 4.

— 684	2
34

3.Разделить единицы:4
ед. : 2 = 2 ед.

Проверить: 2х2=4. Остатка нет.

В частном на месте единиц написать 2.

— 684     8       -4         4	2
342

4.Прочитать ответ:
342.

Второй алгоритм письменного деления
трёхзначного числа на однозначноеДля того чтобы
трёхзначное число 478 разделить на однозначное число 2, надо:

1.Разделить сотни: 4
сот.:2 = 2 сот.

Проверить: 2х2=4. Остатка нет.В частном на месте сотен написать 2.

2.Разделить десятки: 7
дес. на 2. В частном будет 3 дес.

Проверить, сколько десятков мы разделили: 3х2=6. Вычитаем: 7-6=1.
Осталось разделить 1 дес. В частном на месте десятков пишем 3.

— 478	2
23

3.Разделить единицы:
(1 дес. + 8 ед):2 = 18 ед.:2=9 ед.

Проверить: 9х2=18. Остатка нет.

В частном на месте единиц написать 2.\

— 478     6    -18	2
239

4.Прочитать ответ: 239.

Третий алгоритм письменного деления
трёхзначного числа на однозначноеДля того чтобы
трёхзначное число 216 разделить на однозначное число 3, надо:

1.Разделить сотни: 2:3
= 0 (ост.2).

Значит, в частном сотен не будет.Осталось разделить 2 сот., или 20 дес.

2.Разделить десятки: (20
дес. + 1 дес.):3=21 дес.:3=7 дес.

Проверить:7х3=21. Остатка нет. В частном на месте десятков написать 7.

— 216 — 6	3
7

3.Разделить единицы: 6
ед.:3 = 2 ед.

Проверить: 2х3=6. Остатка нет.

В частном на месте единиц написать 2.

— 216      6	3
72

4.Прочитать ответ: 72.Четвёртый алгоритм письменного деления
трёхзначного числана однозначноеДля того чтобы
трёхзначное число 836 разделить на однозначное число 4, надо:

1.Разделить сотни: 8
сот.:4 = 2 сот.

Проверить: 2х4=8. Остатка нет.В частном на месте сотен написать 2.

2.Разделить десятки: 3
дес. на 4. В частном будет 0 дес.

Проверить сколько десятков мы разделили:
0х4=0.Вычесть: 3 – 0 =3. Осталось разделить 3
дес., или 30.В частном на месте десятков написать 0.

3.Разделить единицы:36
ед.:4 = 9 ед.

Проверить: 9х4=36. Остатка нет.

В частном на месте единиц написать 9.

— 836    —36	4
209

4.Прочитать ответ: 209.

Простые и составные значения

В некоторых случаях не всегда возможно воспользоваться специальными таблицами простых чисел. Математики рекомендуют применить одну из методик, которая заключается в следующем:

1. Записать числовое значение.
2. «Прогнать» его по всем признакам делимости.
3. Сделать вывод.

Второй пункт для новичков может показаться не совсем понятным. Однако он подразумевает, что нужно поочередно выполнить операцию для каждого правила. На практике реализация выглядит следующим образом:

1. 287.
2. На 2 не делится (-), поскольку 7 — нечетная цифра.
3. 3: 2+8+7=19 (-).
4. 4: 8+7=15 (-).
5. 5: (-), т. к. заканчивается не на 0 или 5.
6. 6: (-), поскольку во втором и третьем пунктах стоит -.
7. 7: 28−14=14 (+).
8. Вывод: не является простым, поскольку делится на 7.