Как быстро считать в уме: приемы устного счета больших чисел

Числовой луч

Знаете, что такое луч и как он обозначается?

На рисунке (1.) видим луч. Прочитай его название. Какая точка является началом луча? Данный луч разбит штрихами на равные отрезки. Отрезок от 0 до 1 называется единичным отрезком.

На обыкновенном луче обозначены числа, у каждого своё место. Именно такой луч в математике называют числовым.

Определение числового луча

Числовой луч – это луч, на котором точками обозначены натуральные числа.

Поставим на луче AB точку C (2.) Длина отрезка AC числового луча – 5 единичных отрезков, длина отрезка AB – 8 единичных отрезков. Используя числовой луч, сравни отрезки: AC<AB; AC>CB; AC+CB=AB.

Где на отрезке AB (3.) будет находиться точка D, чтобы отрезок AB был меньше отрезка AD на 2 единичных отрезка? Для этого надо из длины отрезка AB отнять 2 единичных отрезка (8-2=6). Точка D будет находиться на делении 6.

Рисунок числового луча:

Используя чертёжную линейку, можно выполнять действия сложения и вычитания. Найдите с помощью числового луча решение задачи, а линейки помогут.

Задача

Велосипедист отправился из пункта А в 6 часов утра. Через 1 час он остановился отдохнуть в придорожном кафе. Спустя 2 часа добрался до конечного пункта. Построить числовой луч и отметить, необходимые для решения задачи, данные.

Сколько времени велосипедист был в пути? Во сколько часов он прибыл в конечный пункт?

А где решение этой задачи?

Задача 2

С помощью линейки построй числовой луч с началом в точке A (используй линейку), укажи на нём точку B (14 см). Найди расположение точек C и D, если отрезок AB короче отрезка AC на 6 см. Отрезок AB длиннее отрезка AD на 10 см. Запишите длину полученных отрезков AC и AD.

Для этого чертим луч с началом в точке A, на луче при помощи линейки находим отметку 14 см, ставим точку B. Мы знаем, что отрезок AB короче отрезка AC на 6 см. Чтобы найти отметку – расположение точки C, надо из 14-6=8 см. На отметке 8 см располагается точка C. Отрезок AB длиннее отрезка AD на 10 см, значит, точка D располагается на отметке 14+10=24 см.

Приведите примеры числовых лучей, которые можно встретить в повседневной жизни.

Числовой луч (картинки):

Этажи в высотном здании тоже своеобразный числовой луч. Особенно во время постепенного возведения стен дома.

Потренируемся

Пример 1. Записать цифрами число, в котором содержится:

1. 55 единиц второго класса и 100 единиц первого класса;
2. 110 единиц второго класса и 5 единиц первого класса;
3. 7 единиц второго класса и 13 единиц первого класса.

Ответ:

1. 55 100;
2. 110 005;
3. 7 013.

Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:

• 10 единиц равны 1 десятку;
• 10 десятков равны 1 сотне;
• 10 сотен равны 1 тысяче;
• 10 тысяч равны 1 десятку тысяч;
• 10 десятков тысяч равны 1 сотне тысяч;
• 10 сотен тысяч равны 1 миллиону.

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.

Пример 2. Сколько сотен содержится в числе 6284?

Как рассуждаем:

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.

Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.

Значит, в данном числе содержится 62 сотни.

Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.

Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

• 11 627 — одиннадцать тысяч шестьсот двадцать семь.
• 31 502 — тридцать одна тысяча пятьсот два.

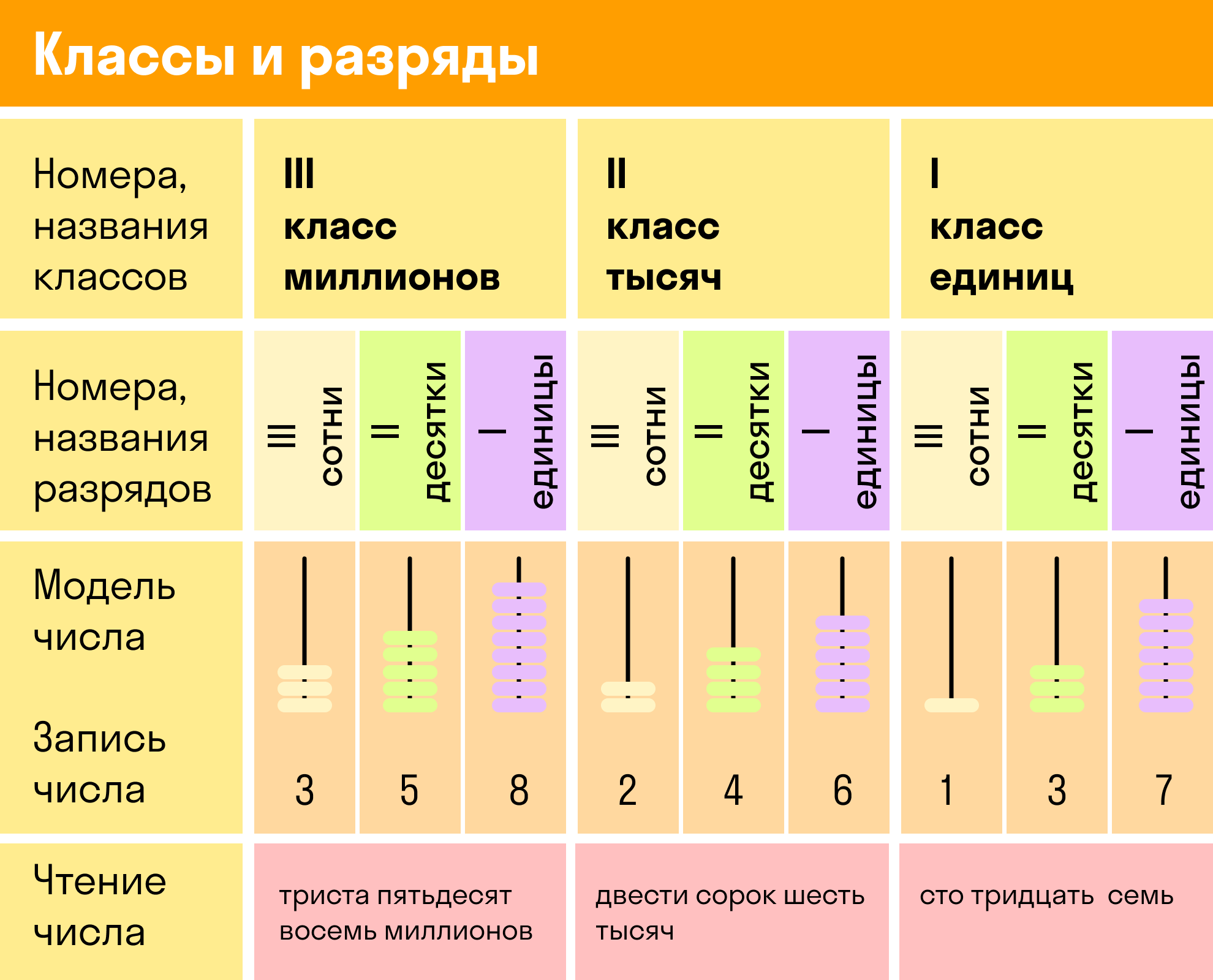
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.

Когда стоит учить ребёнка считать

Большинство специалистов считают, что лучшее время для обучения малышей счёту — это 3–5 лет. Именно в этом возрасте ребёнок начинает интересоваться новым и учится устанавливать закономерности между цифрами. Однако всё очень индивидуально. Если малыш активно осваивает мир и интересуется математикой  раньше, можно начать обучение и с 1,5 лет. 

Какие методики использовать для обучения счёту 

Собрали проверенные методики, которые позволяют сделать это в игровой форме, интересной для ребёнка.

Счёт на пальцах. Методика помогает понять, как научить ребёнка считать до десяти. Запомнить сразу все цифры малышу будет сложно, поэтому можно начать с пяти и ориентироваться на пальцы одной руки. Познакомьте ребёнка с их названиями, далее подключите вторую руку. Можно использовать игры с пальчиками, когда один исчезает или два–три пальчика встречаются вместе.

Использование обучающих карточек и палочек. Можно выкладывать их по одной на стол и называть цифры, потом сдвинуть одну часть палочек вправо, а другую — влево и спросить, сколько палочек в каждой части. 

Игры с цифрами. Обучение детей счёту может проходить в игровой форме. Например, сюжетно-ролевая игра «магазин». Нужно выбрать, кто будет продавцом, а кто — покупателем, и назначить валюту. Продавая или покупая конфеты и игрушки, ребёнок легко запомнит цифры до десяти и даже до двадцати.

Методика Монтессори. Она схожа с игрой в магазин. Можно дать ребёнку разные монеты, например, рубль, два, пять, и попросить его посчитать сумму или разменять деньги.

Методика Домана. Автор рекомендует использовать карточки с красными точками для счёта

Цвет привлечёт внимание малыша.

‍Карточки Глена Домана‍

«Стосчёт». Николай Зайцев предлагает сразу показать  числа от 0 до 99. Так ребёнок поймёт, сколько десятков и единиц составляет каждое число.

‍Карточки Николая Зайцева‍

Методика Полякова. Понадобятся кубики, коробочка с отсеками по количеству кубиков и числа. Сначала берётся один кубик, ставится в ячейку и рядом кладётся цифра 1. И так до 100.

‍Кубики Сергея Полякова‍

Как научить ребёнка считать до 20

Чтобы научить ребёнка считать до 20, используйте две пары рук — ваши и его собственные. Ещё можно задействовать кубики, карточки, палочки или рисовать чёрточки — что придёт в голову. Такой счёт даётся также легко, как и до 10. На этом этапе ребёнку нужно понять состав числа.

<<Блок перелинковки>>

Как научить ребёнка считать до 100

Расскажите ребёнку о том, что десятков всего девять, после этого назовите каждый десяток: десять, двадцать, тридцать и так далее. Предложите ему каждый день заучивать по 10 новых цифр каждого десятка. В конце дня спрашивайте, что ребёнок запомнил, и повторяйте выученное  в другие дни. Упростить повторение можно считая предметы, которые находятся перед вами. После того как ребёнок освоит десятки, предложите ему сыграть в игру: напишите ряд чисел с десятками и пропустите одно число в середине. Попросите ребёнка заполнить пропуск.

<<Форма демодоступа>>

Также можно использовать методику Глена Домана. Сначала ребёнку нужно показывать карточки, где изображено не более пяти точек, затем увеличить их число до 20, 50 и далее до 100. Этот метод поможет также натренировать зрительную память.

Важно обратить внимание ребёнка на числа с 11 до 19, так как они называются отличным от остальных образом

Эта сложная наука – математика

Некоторым деткам научиться математическому счету бывает намного труднее, чем, например, научиться читать. Поэтому, чтобы у ребенка появилась так называемая «симпатия» к предмету, родителям придется постараться привить любовь ребенка к математике.

Некоторые родители не желают обременять себя подобными делами и перекладывают обучение вычислениям на плечи педагогов начальной школы. Безусловно, именно учителя и выполняют обучение счету детей, но родители не должны самоустраняться, а обязаны помогать ребенку, помогать находить ошибки, анализировать их.

Даже если вы решили воспользоваться услугами репетитора, заниматься с ребенком дома все равно придется, ведь учитель задает домашние задания, которые следует добросовестно выполнять. В противном случае знания, не подкрепленные практикой, очень быстро забудутся.

Устный счет с опорой на состав числа

Зная состав числа, ребенок может устно выполнить действия по сложению и вычитанию. Понимая, например, что число 8 состоит из 5 и 3, или 1 и 7, или 6 и 2, или 4 и 4, он может не задумываясь решать задачи на сложение и вычитание с этим числом.

Для лучшего запоминания рекомендуется решать с ребенком несложные задания:

• Раскладывать в 2 коробки определенное количество предметов (например, взять 8 горошин и разложить их в разных вариантах: 5+3, 1+7 и т.д.). Предметы нужно постоянно менять, чтобы у ребенка не пропал интерес.
• Предложить ребенку дополнить число до нужного. Например, повесить на елку 5 игрушек и попросить дополнить елку до 8 игрушек и т.д.

Дальше нужно усложнять задачу и решать примеры “выходящие” за десяток, например 8+5. Для этого нужно:

• Дополнить первое слагаемое до 10. То есть, ребенок уже знает, что 10=8+2. То есть, ему нужно из второго слагаемого “забрать” число 2.
• Он вычисляет, сколько еще нужно добавить (на основе знания состава числа 5 = 2+3);
• Высчитать 8+2+3=13,

Такой же прием (доведение до 10) ребенок будет применять и при вычитании.

Освоив эти способы, ребенок в дальнейшем будет использовать их при решении примеров с числами в пределах 100 и 1000.

Сложение и вычитание

Умение складывать и вычитать вырабатывается обычно к пяти годам. Сначала это следует делать с помощью различных предметов, затем тренироваться решать простейшие примеры в уме. При обучении счету постепенно нужно вводить несложные примеры на сложение и вычитание. Решать примеры столбиком еще рано, но складывать однозначные числа вполне можно научить.

Заниматься математикой с малышом необходимо так, чтобы он не растерял интерес. Поэтому никаких скучных примеров по типу «3+5=? » быть не может. Учим, завлекая, наглядно. Можно в шуточной форме.

Начинать нужно с простого. К примеру, прибавлять к каждой известной цифре единицу и ее же вычитать. Стоит использовать при этом предметы, интересные ребенку или важные для него. Пример представлять лучше в виде вопроса: «У тебя две печеньки. Одной ты поделишься с мамой. Сколько останется у тебя? » И все в таком же духе.

Чтобы переходить к вычитанию, убедитесь, что малыш хорошо освоил сложение. Используйте примеры сложения и вычитания не только на занятиях, но и на прогулке, в магазине, за обедом, при уборке комнаты. Пусть ребенок проговаривает вслед за вами условие задачки. Пользуйтесь специальными пособиями и дидактическими материалами с несложными упражнениями

Обращайте внимание на наличие ярких иллюстраций. Не забываем – ребенка нужно завлечь

Чтобы легко складывать и вычитать, малышу необходимо изучить состав числа. Он должен усвоить, что 5 состоит из цифр 2 и 3, 1 и 4, 10 – из цифр 1 и 9, 2 и 8 и так далее. Перед тем, как научиться правильно считать в уме, ребенок должен хорошо решать задачки с наглядными материалами или на пальцах. Начинать обучение счету про себя лучше с 4 лет, не раньше. С этого возраста время, отведенное на сложение и вычитание, сказывается на общем развитии.

Важно усвоить понятия «больше», «меньше». Пролистывая обучающие книжки, можно спрашивать, каких животных на странице больше, какого цвета меньше

Также нужно выучить термин «поровну». Обязательно нужно объяснить ребенку, что от перемены мест слагаемых сумма не меняется.

Примеры интересных закономерностей

Задания на поиск закономерностей отлично мотивируют детей быстрее освоить арифметику и перейти к заданиям посложнее.

Найди закономерность и определи, какое число спрятал четвёртый робот?

Какое число будет следующим в этом ряду?

Задания на логику гораздо интереснее арифметических тренажёров.

Тренажеры по математике 2 класс (задачи и примеры)

 В математике, конечно же, важно уметь думать и мыслить логически, но не менее важна в ней практика. Половина ошибок на экзаменах по математике делается из-за неправильного вычисления простых действий с числами – сложение, вычитание, умножение, деление. А отработать эти навыки важно еще в начальной школе

Чтобы ничего не упустить, необходимо систематически заниматься с ребенком по специальным тетрадям – тренажерам. Они позволяют отработать математические навыки и умения и довести их до автоматизма. Тренажеры разнообразные, не обязательно скачивать их все, достаточно одного-двух понравившихся. Пособия можно использовать в работе с младшими школьниками не зависимо от программы, по которой ведется обучение

А отработать эти навыки важно еще в начальной школе. Чтобы ничего не упустить, необходимо систематически заниматься с ребенком по специальным тетрадям – тренажерам

Они позволяют отработать математические навыки и умения и довести их до автоматизма. Тренажеры разнообразные, не обязательно скачивать их все, достаточно одного-двух понравившихся. Пособия можно использовать в работе с младшими школьниками не зависимо от программы, по которой ведется обучение.

Один из самых важных моментов математики за 2 класс – отработать до автоматизма таблицу умножения. Отводим этой теме целую страницу. Чтобы перейти на нее и скачать тренажер на таблицу умножения, кликните по картинке:

Далее пособия расположены сверху вниз в порядке увеличения сложности. Чтобы посмотреть и скачать тренажер, кликните по обложке.

Математика. Решаем примеры с переходом через десяток.

Тетрадь для отработки навыков сложения и вычитания с переходом через десяток. Не просто примеры, а интересные игры и задания.

Карточки-задания. Математика. Сложение и вычитание. 2 класс

Удобные карточки для учителя второклашек. 2 варианта на сложение и вычитание одного вида. Подойдут для организации самостоятельной работы по математике в зависимости от продвижения по программе.

Математика. Сложение и вычитание в пределах 20. 1-2 классы. Е.Э.Кочурова

В разных курсах математике тема сложения и вычитание в пределах 20 изучается или в конце 1 класса, или в начале 2-го. В любом случае пособие поможет закрепить изученные способы манипуляций с числами, в некоторых заданиях эти способы представлены в виде своеобразных подсказок. В ходе самостоятельной работы с тетрадью ребенок ориентируется на образец выполнения и алгоритмические предписания. Умение пользоваться такими подсказками в учебе позволит ученику не только находить и использовать нужную информацию в ходе выполнения задания, но и осуществлять самопроверку. 

Начинается тетрадь с отработки навыков сложения и вычитание в пределах 10, эта часть подойдет и для первоклашек.

Математика тренажерная тетрадь для 2 класса

Тетрадь содержит не только примеры на сложение и вычитание, но и перевод единиц друг в друга, и сравнение результатов вычисления (больше-меньше).

3000 примеров по математике (счет в пределах 100 часть 1)

Тренажер со счетом на время. Время засекать на решение одной колонки примеров и записывать внизу в окошечке

Обратите внимание на колонки, которые ребенок решал более 5 минут, значит у него возникли сложности по этому виду примеров. Приведены примеры на сложение и вычитание в пределах десяти и с переходом через десяток,  сложение и вычитание десятков, манипуляции в пределах сотни. В этой прописи дается много примеров на сложение и вычитание, чтобы закрепить навыки устного счета в пределах 100

В этой прописи дается много примеров на сложение и вычитание, чтобы закрепить навыки устного счета в пределах 100.

Считаем правильно. Рабочая тетрадь по математике. Г.В.Белых

Тетрадь также выполнена в виде тренажера, сплошные примеры и уравнения.  Начинается со счета в пределах десяти, далее – в пределах сотни (сложение, вычитание, умножение и деление), заканчивается сравнением уравнений (примеры со знаками больше, меньше, равно).

Пособия пригодятся и учителям начальных классов в их работе, и родителям для занятий дома с детьми, в частности, в летние каникулы. Задания разных уровней сложности позволят осуществить дифференцированный подход к обучению.

А еще у нас есть отличный онлайн тренажер по математике! Родителям не нужно ничего распечатывать и проверять, все это за вас совершенно бесплатно сделаем мы! Выбирайте режим и вперед >>

Как правильно научить ребёнка считать столбиком

Объясните, что в сложении и вычитании все действия производят по разрядам: десятки с десятками, единицы с единицами. Например, 31+12: тройка складывается с единицей, единица с двойкой. 

Для упрощения можно  делать  тренировочные упражнения — например, записывать числа друг под другом. Внизу цифра 6, вверху 12

Важно объяснить ребёнку, что шесть должна стоять под цифрой 2, а не 1, так как относится к единицам

Начните с простых примеров, где цифры при сложении образуют число меньше 10. Дальше можно переходить к примерам с переходом через десяток: например, 25+16. 5+6 в сумме дают 11. Тогда единицу от 11 мы пишем под чертой, а единицу в качестве десятка мы запоминаем. Когда складываем десятки, получаем 2+1 и ещё +1, который мы держали в голове.

В случае с вычитанием нужно также начать с простых примеров, постепенно переходя к более сложным. Например: 25−16, в столбике, где стоят единицы, 5 меньше 6, объяснить ребёнку, что в этом случае мы как бы «занимаем» у десятков единицу.

Для удобства можно использовать обозначения, которые на рисунке отмечены голубым. В первом случае дописан десяток, во втором — точка служит напоминанием о «зАнятом» десятке. 

Ход НОД

Игровая ситуация.

-Ребята сегодня с вами мы отправимся в путешествие в лес.

Давайте мы туда отправимся на паровозе. Дети строятся за воспитателем. Раздается гудок, паровоз отправляется, проехав круг по группе, останавливается.

Вот мы и приехали в лес. На фланелеграф расположен

лес и избушка.

Ребята вы не знаете, кто здесь живет?

А хотите узнать? (ответы детей)

Тогда отгадайте загадку.

Возле леса на опушке

Трое их живет в избушке.

Там три стула и три кружки,

Три кровати, три подушки.

Угадайте без подсказки,

Кто герои этой сказки? (Три медведя)

Да ребята на лесной опушке живут медведи (воспитатель выставляет на фланелеграф двух медведей).

-Сколько медведей на опушке? Давайте посчитаем(1,2).

-А вот к ним прибежал еще Мишутка.

-Сколько стало медведей? (3).

Получается, два да еще один (3)

-Ребята, давайте вместе посчитаем медведей. (1.2.3).

Ох, ребята мы считали и немножко устали. Медвежата предлагают нам немного поиграть. Раз, два повернись и в медвежонка превратись.

Физминутка:

Медведи по лесу шли (дети шагают вперевалочку).

Впереди большой медведь (Поднимают руки над головой, тянут их вверх).

Посередине шла медведица (Руки ставят на пояс, делая пружинку).

Мишутка плелся позади (присев, качаются).

Шли все они вразвалочку, собирая палочки,

(дети имитируют медведя вразвалочку, наклоняясь, подбирая палочки).

Поиграли медведи, и захотелось им покушать (воспитатель выставляет тарелки на фланелеграф).

-Ребята кому мы поставим самую большую тарелку? (ответы детей)

Сколько на столе тарелок? (1)

Кому поставим вторую тарелку? (ответы детей)

Сколько стало тарелок? (2).

Ну и кому же достанется самая маленькая тарелка? (ответы детей).

Сколько стало тарелок? (3).

-Что можно сказать о количестве медведей и тарелок? (их поровну).

На основе счета ребята убеждаются в равенстве медведей и тарелок.

-Ребята давайте с вами вспомним сказку. На чем сидели медведи?

У Михайло Ивановича, какой был стул? (воспитатель показывает большой стул). (Ответы детей)

Какой стул у Настасьи Петровны? (поменьше).

У Мишутки, какой стул? (маленький).

-Молодцы всем распределили стулья.

Сейчас предлагаю поиграть

Игра «Что изменилось».

На доске расположен числовой ряд от 1 до 3. Дети закрывают глаза, воспитатель в это время убирает цифру 2. Открыв глаза, они должны сказать, что изменилось, какая цифра пропала. Пропавшую цифру ставят в ряд. При повторном проведении игры цифру убирает кто — то из детей. В первый раз следует убрать именно цифру 2, так как дети должны увидеть границы числового ряда.

Игра «У медведя в бору»

Рефлексия: Ребята, где мы сегодня с вами побывали?

Сколько медведей было в сказке?

С какой цифрой мы познакомились?

Куда бы вы хотели отправиться завтра?

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить.  Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Двузначные числа и их запись

Друзья, я запутался! Пытался записать двузначные числа и всё забыл! Помогите!

Давайте напомним, какие числа именуются двузначными. Чтобы их написать потребуется пара знаков – цифр двузначного числа. Правая цифра обозначает разряд единиц, а левая – разряд десятков. 30 и 30 можно назвать равными двузначными числами, так как количество десятков и единиц одинаковое.

Арифметический диктант

Запишите двузначное число, равное числу из 4 десятков и 6 единиц.

4 д. 6 ед. = 46

Приведите пример двузначного числа больше, чем 9 на 10.

Слово «больше» указывает на действие сложение, значит 9+10=19. Искомое число – 19.

Из наибольшего двузначного числа отнимите наименьшее двузначное число.

Решение будет следующим: 99-10=89

Прочитайте ответы, начиная от самого большого к самому маленькому двузначному числу. Полученные ответы: 46, 19, 89. Наименьшее из этих чисел 19, за ним при счёте следует 46 и последним – 89.

Задание для знатоков

1. Используя только цифры, которые обозначают чётные числа (2, 4, 6, 8), составить двузначные числа.

Для написания применили чётные числа. Если число оканчивается цифрами 0, 2, 4, 6, 8, то оно считается чётным.

1. Записать, начиная с наименьшего двузначного числа.

Используя записанный ряд чисел, приведи пример двузначного числа, которое больше всех остальных.

Для проверки: 22 24 26 28 42 44 46 48 62 64 66 68 82 84 86 88.

Загадка

Используя однозначные и двузначные числа в порядке возрастания, нарисовать ответ на загадку.

Она кудахчет по утрам, Неся яйцо в подарок нам.

Напиши самое большое двузначное число, которое использовалось для рисования. 

Сложение двузначных чисел

Музыкальная пауза!

Учите, детки, математику!

Старательней вникайте в суть…

Гоните лень, усвойте тактику –

Учить предмет не как-нибудь.

А я хочу, а я хочу опять…

Заполни пропуски в таблице:

Сложение двузначных чисел без перехода через десяток

Для удобства выполнения действий можно применять запись в столбик.

Схема действий:

1. Записываю цифру единиц под разрядом единиц, а цифру десятков – под разрядом десятков.
2. Выполняю сложение единиц, результат пишу под разрядом единиц.
3. Выполняю сложение десятков, результат пишу под разрядом десятков.
4. Называю результат.

Найдите суммы чисел, записанных в столбик:

Вычитание двузначных чисел без перехода через десяток

Чтобы найти разность двузначных чисел, можно использовать запись столбиком.

Схема действий:

1. Записываю цифру единиц под разрядом единиц, а цифру десятков – под разрядом десятков.
2. Выполняю вычитание единиц, результат записываю под единицами.
3. Выполняю вычитание десятков, результат записываю под десятками.
4. Называю результат.

Найдите разность двух чисел, записанных в столбик:

Приемы сложения и вычитания вида□ + 6, 7, 8, 9, □–6, 7, 8, 9

Поселились все зверюшки вместе в теремке. И дружно вместе принялись записывать остальные таблицы. Все примерах в них составляются на основе тех правил, о которых напомнила нам лисичка. Давай поможем им.

Начнем с таблицы сложения числа 6.

В предыдущих таблицах есть только четыре примера, в которых встречается слагаемое 6. Найди их.

Вот что выписали зверята.

Теперь переставляем слагаемые местами.

А теперь из этой таблицы мы легко можем составить таблицу вычитания числа 6. Попробуй сделать это самостоятельно.

Посмотри, какую таблицу вычитания числа 6 записали наши друзья.

Вот мы и закончили! У нас получилось составить таблицы сложения и вычитания числа 6.

Продолжаем. С таблицей сложения числа 7 нам повезло еще больше, ведь в ней будет всего три примера. Ты уже нашел их? Вот что записали зверята.

Надеюсь, ты не забыл еще переместительное свойство действия сложения, ведь оно нам пригодится при составлении таблицы с числом 7.

Подумай над этим сам. А потом проверь.

Все правильно. Теперь из предыдущей таблицы составим таблицу вычитания числа 7.

Не спеши, сделай это самостоятельно.

Проверь свою таблицу.

Как быстро ты со всем справился.

Дальше будет еще легче. Вспомни примеры, где встречается слагаемое 8.

В таблице сложения числа 8 всего два примера. Составь их.

Давай проверим.

Теперь составь таблицу вычитания числа 8.

Вот что получилось у наших друзей.

Вот мы и выучили таблицы сложения и вычитания с числом 8.

Ты, наверное, уже немного устал. Но нам осталось познакомиться всего с одной таблицей. Это таблица сложения и вычитания с числом 9.

Ты уже нашел пример с числом 9? Уверена, что ты справился. Назови его.

9 + 1 = 10

Давай переставлять. Что у нас получится?

1 + 9 = 10

Вот и вся таблица сложения с числом 9. Переходим к таблице вычитания числа 9.

У тебя уже все готово?

Правильно.

10 − 9 = 1

Мы с тобой неплохо потрудились и составили все таблицы в пределах 10. Вот как выглядит общая таблица сложения.

В этой таблице красным цветом выделены примеры, которые составлены путем перестановки слагаемых. Их запомнить очень легко.

А вот общая таблица вычитания чисел в пределах 10.

В этой общей таблице хорошо видны несколько закономерностей, которые помогут тебе лучше и быстрее запомнить результаты указанных математических выражений на вычитание.

1. В результате вычитания числа 1 получается число, которое является предыдущим по отношению к уменьшаемому.
2. В примерах, где уменьшаемое и вычитаемое являются «соседями» в натуральном ряду чисел, разность равна 1.
3. В таблице есть «парные» примеры, которые можно составить из одного и того же примера на сложение.

В этих выражениях компонентами являются одни и те же числа. Присмотрись и найди другие подобные пары примеров.

Чтобы получше запомнить все примеры из таблиц сложения и вычитания чисел в пределах 10, почаще тренируйся. Не забудь о наших сегодняшних помощниках.

Таблицы сложения и вычитания числа 1 мы выучили с помощью мышки, которая переходила маленькими шагами с числа на соседнее число. Как найти результаты в таблицах сложения и вычитания числа 2 нам подсказала лягушка, которая умеет прыгать через число. Зайчик показал, как узнать ответы в примерах из таблиц сложения и вычитания числа 3, который скачет так высоко, что может перепрыгнуть через два числа сразу. А двойной прыжок лягушки поможет вспомнить результаты таблиц сложения и вычитания числа 4. Лисичка же разгадала закономерности составления всех остальных таблиц.

Обязательно используй все приемы, которые нам подсказали герои нашей сказки. Чем чаще ты будешь повторять примеры из таблиц, тем быстрее ты запомнишь результаты каждого из них. Надеюсь, ты легко справишься с проверочными заданиями к этому уроку.

Считаем и решаем примеры до 20

Когда счет до 10 был освоен и ребенок стал свободно ориентироваться в первой десятке цифр, наступает время переходить на новый этап и обучаться двузначным числам, считать примеры в пределах 20.

Запоминаем цифры

Чтобы ребенок хорошо запоминал последовательность цифр, лучше всего использовать 20 одинаковых предметов (это даст возможность наглядно все объяснять малышу) или опять же карточки с числами.

Выглядеть это будет так:

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20

Поясняем ребенку, что в числах после 10 есть сходство. Визуализируя таким образом числа и десятки, вы поможете ребенку эффективнее запомнить их последовательность и названия. Видим число 11 – говорим «один» и прибавляем окончание «надцать». Так же поступаем и с другими двузначными числами – «три-надцать», «пять-надцать», «шесть-надцать» и т. д.

Работайте с ребенком на повторение, пока он не запомнит названия чисел.

Решаем примеры

Прежде чем приступить к решению примеров и обучению в пределах двадцати, дошкольник должен уяснить такие понятия, как «десятки» и «единицы». Для начального этапа обучения можно использовать кубики, палочки или попробовать учиться на счетах, а потом уже приучать малыша считать в уме. В возрасте 5 или 6 лет он должен уметь считать без помощи пальцев и других посторонних предметов.

Для первых занятий лучше использовать такие упражнения для детей, в которых не нужно совершать вычисления с переходом через десяток. Подойдут примеры, где все математические действия происходят с целым десятком или десятками и с некоторым количеством единиц, которые прибавляются либо вычитаются.

То есть десяток – основа всего примера.

Сложите кубики, палочки или другие предметы, с которыми вы работаете, по порядку в количестве 10 штук. Объясните малышу, что это десяток. Потом попросите прибавить к этому количеству еще несколько предметов, допустим 4. Говорите: «Десять плюс четыре равно четырнадцать». После того, как вы научили ребенка складывать, подобным образом составьте примеры с вычитанием, например:

18-8=10

13-10=3 и т. д.

Следующий этап – вычисления с переходом через десяток. Такие примеры даются ребятам несколько сложнее. Здесь уже понадобятся знания не только целых десятков и отдельных единиц, но и общее представление состава отдельного числа.

• Из чего состоит число 3? Из 1 и 2, или 1 и 1 и 1.
• А что такое 7? Это 1+6= 2+5= 1+1+1+4 и т. д.

Подобным образом поступите со всеми числами, которые знает ребенок, разберите их на составляющие части. Потом эти знания хорошо применить в решении примеров.

Разберем такой пример:

4+9=

Второе слагаемое раскладываем на два составляющих числа, чтобы при сложении с первым слагаемым получить десятку, а потом прибавляем остаток:

4+(6+3)= 10+3=13, т. е. 4+9= 13

Закрепим знания еще несколькими примерами:

5+7=

5+(5+2)= 10+2= 12

или

8+9=

8+(2+7)= 10+7= 17

Таким же образом можно решать примеры с вычитанием:

16-7=

16-(6-1)= 10-1= 9

или

13-8=

13-(3-5)= 10-5= 5

То есть для того чтобы сделать вычисление, раскладываем второе слагаемое таким образом, чтобы при вычитании из первого слагаемого получилась десятка, а потом вычитаем оставшееся число.

Также удобно показать малышу работу со сложением и вычитанием в столбик. В таких примерах нагляднее видно десятки и единицы, что с чем складывать или вычитать.

Напоследок несколько рекомендаций родителям.

• Во время занятий математикой проявите терпение к своему маленькому ученику и не раздражайтесь от его непонимания, а тем более не кричите.
• Не давите на ребенка и не заставляйте заниматься, если ему не хочется. Отпустите его, ведь он все равно не сконцентрируется. А в следующий раз придумайте, как его заинтересовать занятиями.
• Контролируйте время занятий, не держите малыша часами за решением примера. 10-20 минут должно длиться одно занятие. Дети быстро теряют концентрацию, и долговременные занятия нельзя назвать эффективными.
• На досуге между делом постоянно тренируйтесь с малышом. Когда режете торт, считайте, сколько кусков получилось, когда сервируете стол, посчитайте количество гостей и попросите принести нужное количество тарелок и т. д.

Главное одно – спокойная обстановка, терпение и родительская любовь однажды все равно дадут положительный результат. Не равняйтесь на других, а занимайтесь своим ребенком. Помните, что все дети разные и всем нужен индивидуальный подход.

Состав числа до 20 — Распечатать и заполнить таблицу

Чтобы распечатать состав числа до 20 в виде числовой таблицы, скачайте файл задания во вложениях (если занятие проводится с группой детей, то распечатайте каждому ребенку по одному экземпляру). Объясните детям, по какому принципу нужно заполнять каждую таблицу:

• В первой таблице ты должен к единичке прибавить число из правого столбика (по порядку), а ответ вписать в пустую клетку слева. И так в каждой строке, пока не дойдешь до самого низа. 
• Во второй таблице нужно прибавлять числа к двоечке.
• В третьей таблице нужно от каждого числа слева отнять единичку, а ответы записать в пустые клетки справа.
• В четвертой таблице от каждого из чисел слева нужно отнимать двоечку.
• В пятой таблице — к тройке прибавлять числа справа.
• И наконец, в шестой таблице тебе нужно от каждого числа слева отнять троечку.

Скачать упражнение «Состав числа до 20 — Распечатать числовую таблицу» вы можете во вложениях внизу страницы.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6.  Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084